Teoria del campo cristallino: differenze tra le versioni

La teoria del campo cristallino, introdotta originariamente dai fisici Hans Bethe e John Hasbrouck van Vleck negli anni 1930, è un modello teorico adottato per interpretare il legame chimico che intercorre nei complessi. Questa teoria rende conto di alcune proprietà caratteristiche di questi composti quali quelle magnetiche, la peculiare colorazione e alcune caratteristiche spettroscopiche e termodinamiche. D'altro canto diviene approssimata o insufficiente nella trattazione più approfondita delle proprietà fisiche e dei legami chimici, come quelli che intercorrono tra un metallo di transizione e un ligando molecolare quale può essere il monossido di carbonio. La teoria del campo dei ligandi rappresenta un altro modello più completo ed esauriente fondato sulla teoria degli orbitali molecolari che riesce a colmare le lacune inerenti alla teoria del campo cristallino rappresentando una sua estensione.

Teoria

Il modello del legame chimico nei complessi assume che i ligandi si avvicinino agli orbitali d del metallo centrale lungo la terna degli assi cartesiani. In questo modo gli orbitali di valenza di quest'ultimo, i cinque orbitali degeneri d, interagiscono con gli elettroni dei ligandi in fase di avvicinamento mutando il loro stato degenere. In pratica i ligandi vengono considerati come cariche negative in fase di avvicinamento.

Diagramma che mostra la separazione energetica degli orbitali nel campo ottaedrico.

Nel caso di complessi ottaedrici, ovvero in generale complessi del tipo ML₆ (M=metallo ed L=ligando) o assimilabili, la simmetria caratteristica produce una nuova coppia di orbitali una doppiamente degenere e l'altra triplamente degenere. La coppia doppiamente degenere è formata dagli orbitali d_z² e d_x²-y² che essendo orientati lungo gli assi cartesiani subiscono un incremento energetico dovuto alla repulsione elettronica generata dall'avvicinamento dei ligandi. Invece gli orbitali disposti lungo i tre piani individuati dagli assi cartesiani, ovvero i d_xy, d_yz e d_xz, sperimentano una minore repulsione e quindi il loro livello energetico risulta inferiore a quello corrispondente allo stato degenere originario. Nel caso in oggetto, ovvero quello di un complesso ottaedrico, gli orbitali doppiamente degeneri sono denominati e_g e hanno carattere antilegante, mentre quelli triplamente degeneri costituiscono gli orbitali t_2g e possiedono natura non legante.

La differenza di energia tra gli e_g e i t_2g viene indicata come Δ_o (delta ottaedrico) e dipende tra l'altro sia dalla natura e stato di ossidazione del metallo che dalla natura e arrangiamento del ligando attorno al centro metallico. La serie spettrochimica elenca un insieme di ligandi in funzione della crescente tendenza a provocare una separazione energetica Δ_o maggiore.

Alto spin e basso spin

Come già detto, in relazione a un dato ione metallico ligandi differenti provocano una differente separazione energetica degli orbitali d all'interno di un campo di definita simmetria. Nel riempire questi nuovi orbitali, sempre in base al principio dell'Aufbau, quando il numero di elettroni è maggiore di tre è possibile sistemare quest'ultimi in due modi differenti. Nel fare ciò occorre considerare quantitativamente l'entità della separazione energetica Δ (per esempio, il Δ_o per complessi ottaedrici o il Δ_T per quelli tetraedrici, per i quali vale Δ_T ≈ 0,45Δ_o) e la cosiddetta energia di accoppiamento di spin, ovvero il surplus energetico derivante da una configurazione con spin antiparalleli (maggiore repulsione).

Configurazione di un complesso ad alto spin quale [FeBr₆]³⁻

Configurazione di un complesso a basso spin quale [Fe(NO₂)₆]³⁻

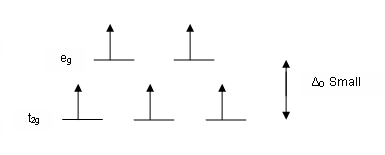
Nello specifico, se la separazione energetica è di minore entità rispetto all'energia di accoppiamento di spin (campo debole) si avrà un maggiore guadagno energetico, e quindi di stabilità, con la disposizione degli elettroni che attuano il semiriempimento secondo la regola di Hund popolando i livelli energetici superiori e_g. In questo modo la molteplicità di spin è massima e si ottiene quello che viene definito complesso ad alto spin. Se invece l'entità della separazione energetica è grande (campo forte) allora risulta più semplice e conveniente l'accoppiamento di spin antiparalleli con produzione di una configurazione con minore molteplicità totale di spin. Il genere di complessi caratterizzati da questa configurazione viene definito a basso spin.

È interessante notare come l'analisi della configurazione elettronica dei complessi possa predire molto semplicemente alcune proprietà fisiche quali quelle magnetiche o spettroscopiche. Un composto che presenta elettroni spaiati è paramagnetico, mentre la presenza di elettroni appaiati conferisce proprietà diamagnetiche. Conoscendo invece il valore della separazione energetica Δ è possibile risalire, tenendo conto che l'assorbimento di un quanto di luce promuove elettroni dagli orbitali t_2g a quelli e_g, alla lunghezza d'onda della radiazione assorbita. Si spiega in tal modo la peculiare colorazione dei complessi (tale lunghezza d'onda ricade nel campo della radiazione visibile) nonché le variazioni di colore legate alla presenza di ligandi differenti legati a uno stesso centro metallico.

Energia di stabilizzazione del campo cristallino

L'energia di stabilizzazione del campo cristallino (CFSE, dall'inglese crystal field stabilization energy) rappresenta il guadagno in stabilità che si ottiene dalla nuova collocazione degli elettroni negli orbitali che hanno mutato i loro livelli energetici a seguito dell'effetto della carica dei ligandi.

Rimanendo nel caso dei complessi ottaedrici, ogni elettrone presente su un orbitale t_2g dà un contributo alla CFSE pari a 0,4Δ_o, mentre il contributo di un elettrone presente su un orbitale e_g corrisponde a 0,6Δ_o. Apllicando il calcolo della CFSE al caso dei complessi d^{5 del ferro mostrati nelle due immagini sopra, rispettivamente si ottiene: nel caso del complesso a basso spin (5 elettroni disposti tutti negli orbitali t_2g), CFSE = 5x0,4 Δ_o = 2Δ_o (in realtà a questo valore occorre sottrarre l'energia di accoppiamento di spin); nel caso del complesso ad alto spin si hanno 3 elettroni nei t_2g (orbitali ad energia inferiore rispetto a quella degli d degeneri) e 2 elettroni negli e_g (ad energia superiore rispetto agli orbitali d degeneri), per cui risulta CFSE = (3x0,4 Δ_o) - (2x0,6 Δ_o) = 0.}

Bibliografia

• D.F. Shriver, P.W. Atkins, Inorganic Chemistry, Oxford University Press, 2001.
• C.E. Housecroft, A.G. Sharpe, Inorganic Chemistry, Pearson Education Limited, 2005. ISBN 0-13-039913-2.
• G.L. Miessler, D.A. Tarr, Inorganic Chemistry, Pearson Prentice Hall, 2003. ISBN 0-13-035471-6.

Voci correlate

• Complesso
• Legame di coordinazione
• Effetto Jahn-Teller
• Teoria del campo dei ligandi