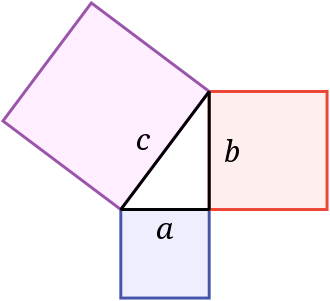
直角邊 的平方和等於斜邊 的平方畢氏定理 (英語:Pythagorean theorem / Pythagoras' theorem )是平面幾何 中一個基本而重要的定理 。畢氏定理說明,平面 上的直角三角形 的兩條直角邊的長度(較短直角邊古稱勾長、較長直角邊古稱股長)的平方 和等於斜邊長(古稱弦長)的平方。反之,若平面上三角形中兩邊長的平方和等於第三邊邊長的平方,則它是直角三角形(直角所對的邊是第三邊)。畢氏定理是人類早期發現並證明的重要數學定理之一。
此定理又稱勾股定理 、商高定理 、畢達哥拉斯定理、新娘座椅定理 或百牛定理 。「畢氏」所指的是其中一個發現這個定理的古希臘數學家畢達哥拉斯 ,但歷史學家相信這個定理早在畢達哥拉斯出生的一千年前已經在世界各地廣泛應用。不過,現代西方數學界統一稱呼它為「畢達哥拉斯定理」。日本除了翻譯西方的「畢達哥拉斯之定理」外亦有「三平方之定理」的稱呼。
早在有明文描述此定理前,古埃及 在公元前 1600年的紙莎草 記載有
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
畢氏三元數 ,而古巴比倫 泥板紀錄的最大的一個畢氏三元數組是
(
12709
,
13500
,
18541
)
{\displaystyle (12709,13500,18541)}
現在畢氏定理可考的嚴謹數學證明,起源於略晚於畢德格拉斯的歐幾里得 幾何原本 中,卷一命題47。但奇怪的是,這個定理從未被叫做「歐幾里得定理」。
《周髀算經 》中,用商高 與周公 對談的方式,提出
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
[ 1] [ 2]
有些參考資料提到法國和比利時將畢氏定理稱為驢橋定理 ,但驢橋定理是指等腰三角形 的二底角相等,非畢氏定理[ 3]
畢氏定理有四百多個證明,如微分證明,面積證明等。
在平面上的一個直角三角形中,兩個直角邊邊長的平方加起來等於斜邊長的平方。如果設直角三角形的兩條直角邊長度分別是
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
或
a
2
+
b
2
=
c
{\displaystyle {\sqrt {a^{2}+b^{2}}}=c}
餘弦定理 是畢氏定理的一個推廣[ 4] 證明 方法,是數學定理 中證明方法最多的定理之一[ 5]
如果
c
{\displaystyle c}
長度 而
a
{\displaystyle a}
b
{\displaystyle b}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
如果
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
c
=
a
2
+
b
2
.
{\displaystyle c={\sqrt {a^{2}+b^{2}}}.\,}
如果斜邊的長度
c
{\displaystyle c}
a
{\displaystyle a}
b
{\displaystyle b}
a
=
c
2
−
b
2
.
{\displaystyle a={\sqrt {c^{2}-b^{2}}}.\,}
或
b
=
c
2
−
a
2
.
{\displaystyle b={\sqrt {c^{2}-a^{2}}}.\,}
簡單來說,只要知道直角三角形的其中兩條邊長,便能求出第三條邊長。
畢氏三元數組 是滿足畢氏定理
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
正整數 組
(
a
,
b
,
c
)
{\displaystyle (a,b,c)}
a
,
b
,
c
{\displaystyle a,b,c}
畢氏三元數 。例如
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
任意一組畢氏三元數
(
a
,
b
,
c
)
{\displaystyle (a,b,c)}
a
=
k
(
m
2
−
n
2
)
,
b
=
2
k
m
n
,
c
=
k
(
m
2
+
n
2
)
{\displaystyle a=k(m^{2}-n^{2}),b=2kmn,c=k(m^{2}+n^{2})}
k
,
m
,
n
∈
N
∗
,
m
>
n
{\displaystyle k,m,n\in \mathbb {N*} ,m>n}
公元前18世紀記錄各種畢氏三元數組的巴比倫石板 這個定理的歷史可以被分成三個部份:發現畢氏三元數 、發現直角三角形 中邊長的關係、及其定理的證明。
畢氏三元數的發現時間較早,例如埃及的紙草書裏面就有
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
(
13500
,
12709
,
18541
)
{\displaystyle (13500,12709,18541)}
[ 6] 周髀算經 》中也記述了
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
[ 7] 金朝 數學家李冶 在《測圓海鏡 》中,通過勾股容圓 圖式的十五個勾股形和直徑的關係,建立了系統的天元術 ,推導出692條關於勾股形的各邊的公式,其中用到了多組畢氏三元數作為例子。
巴比倫人得到的畢氏三元數的數量和質量不太可能純從測量手段獲得。之後的畢達哥拉斯 本人並無著作傳世,不過在他死後一千年,5世紀的普羅克勒斯 給歐幾里德 的名著《幾何原本 》做註解時將最早的發現和證明歸功於畢達哥拉斯學派 :
“
如果我們聽聽那些喜歡說古代歷史的人,他們把這個定理歸於畢達哥拉斯,並且說他殺了一百頭公牛來慶祝。對我來說,雖然我欣賞那個第一個觀察到這個定理的人,我更嘆服《原本》的作者。不光是因為他給出了清晰明確的證明,而且還因為他用無可置疑的方法在第六篇中證明了一個更一般的命題。
”
普魯塔克 和西塞羅 也將發現的功勞歸於畢達哥拉斯,但沒有任何證據表明畢達哥拉斯證明了畢氏定理,以素食 聞名的畢達哥拉斯殺牛更是不可思議。
在中國,記載秦朝的算數書 並未記載畢氏定理,只是記錄了一些畢氏三元數。定理首次載於書面則是在成書於西漢但內容收集整理自公元前一千多年以來的《周髀算經 》「榮方問於陳子」一節中:
“
若求邪至日者,以日下為勾,日高為股,勾股各自乘,並而開方除之,得邪至日。
”
——《周髀算經 》卷上之二
因此此定理也被稱之為陳子定理。
東漢末年趙爽 《周髀算經 注》《勾股圓方圖注》記載:
“
勾股各自乘,並之,為弦實,開方除之,即弦。
”
趙爽 《勾股圓方圖》在《九章算術 注》中,劉徽 反覆利用畢氏定理求圓周率 ,並利用「割補術」做「青朱出入圖 」完成畢氏定理的幾何圖形證明。
直至現時為止,仍有許多關於畢氏定理是否不止一次被發現的辯論。
畢達哥拉斯學派的證明沒有流傳下來,流傳下來書面證明最早見於《幾何原本》第一冊的第47個命題。在中國,東漢末年吳國的趙爽 最早給出畢氏定理的證明。巴勒蒂·克爾什納·蒂爾特吉 吠陀數學 一書中聲稱古代印度教吠陀證明了畢氏定理。
這個定理有許多證明的方法,其證明的方法可能是數學眾多定理中最多的。路明思(Elisha Scott Loomis)的Pythagorean Proposition 一書中總共提到367種證明方式。
有人會嘗試以三角恆等式 (例如:正弦 和餘弦 函數的泰勒級數 )來證明畢氏定理,但是,因為所有的基本三角恆等式都是建基於畢氏定理,所以不能作為畢氏定理的證明(參見循環論證 )。
中國三國 時期趙爽 為證明畢氏定理作「勾股圓方圖」即「弦圖」,按其證明思路,其法可涵蓋所有直角三角形,為東方特色畢氏定理無字證明法。2002年第24屆國際數學家大會 (ICM)在北京 召開。中國郵政 發行一枚郵資明信片,郵資圖就是這次大會的會標—中國古代證明畢氏定理的趙爽弦圖。
趙爽 勾股圓方圖證明畢氏定理法動畫 中國魏晉 時期數學家劉徽 依據其「割補術」為證畢氏定理另闢蹊徑而作「青朱出入圖 」。劉徽描述此圖,「勾自乘為朱方,股自乘為青方,令出入相補,各從其類,因就其餘不動也,合成弦方之冪。開方除之,即弦也。[ 8]
劉徽 青朱出入圖 相似三角形的證明 有許多畢氏定理的證明方式,都是基於相似 三角形中兩邊長的比例 。
設
A
B
C
{\displaystyle ABC}
∠
C
{\displaystyle \angle C}
C
{\displaystyle C}
高 ,並將此高與
A
B
¯
{\displaystyle {\overline {AB}}}
H
{\displaystyle H}
△
A
C
H
{\displaystyle \bigtriangleup ACH}
△
A
B
C
{\displaystyle \bigtriangleup ABC}
A
{\displaystyle A}
△
C
B
H
{\displaystyle \bigtriangleup CBH}
△
A
B
C
{\displaystyle \bigtriangleup ABC}
因為
B
C
¯
=
a
,
A
C
¯
=
b
,
and
A
B
¯
=
c
,
{\displaystyle {\overline {BC}}=a,{\overline {AC}}=b,{\text{ and }}{\overline {AB}}=c,\!}
所以
a
c
=
H
B
¯
a
and
b
c
=
A
H
¯
b
.
{\displaystyle {\frac {a}{c}}={\frac {\overline {HB}}{a}}{\text{ and }}{\frac {b}{c}}={\frac {\overline {AH}}{b}}.\,}
可以寫成
a
2
=
c
×
H
B
¯
and
b
2
=
c
×
A
H
¯
.
{\displaystyle a^{2}=c\times {\overline {HB}}{\text{ and }}b^{2}=c\times {\overline {AH}}.\,}
綜合這兩個方程式,我們得到
a
2
+
b
2
=
c
×
H
B
¯
+
c
×
A
H
¯
=
c
×
(
H
B
¯
+
A
H
¯
)
=
c
2
.
{\displaystyle a^{2}+b^{2}=c\times {\overline {HB}}+c\times {\overline {AH}}=c\times ({\overline {HB}}+{\overline {AH}})=c^{2}.\,\!}
換句話說:
a
2
+
b
2
=
c
2
.
{\displaystyle a^{2}+b^{2}=c^{2}.\,\!}
《幾何原本》中的證明 在歐幾里得 的《幾何原本 》一書中給出畢氏定理的以下証明。設
△
A
B
C
{\displaystyle \bigtriangleup ABC}
A 為直角。從
A
{\displaystyle A}
在定理的證明中,我們需要如下四個輔助定理:
如果兩個三角形有兩組對應邊和這兩組邊所夾的角相等,則兩三角形全等。(SAS定理)
三角形面積是任一同底同高之平行四邊形面積的一半。
任意一個正方形的面積等於其二邊長的乘積。
任意一個矩形的面積等於其二邊長的乘積(據輔助定理3)。 證明的思路為:把上方的兩個正方形,透過等高同底的三角形,以其面積關係,轉換成下方兩個同等面積的長方形。
證明輔助圖2 其證明如下:
設
△
A
B
C
{\displaystyle \triangle ABC}
∠
C
A
B
{\displaystyle \angle CAB}
其邊為
B
C
¯
{\displaystyle {\overline {BC}}}
A
B
¯
{\displaystyle {\overline {AB}}}
C
A
¯
{\displaystyle {\overline {CA}}}
C
B
D
E
{\displaystyle CBDE}
B
A
G
F
{\displaystyle BAGF}
A
C
I
H
{\displaystyle ACIH}
畫出過點
A
{\displaystyle A}
B
D
¯
{\displaystyle {\overline {BD}}}
C
E
¯
{\displaystyle {\overline {CE}}}
B
C
¯
{\displaystyle {\overline {BC}}}
D
E
¯
{\displaystyle {\overline {DE}}}
K
{\displaystyle K}
L
{\displaystyle L}
分別連接
C
F
¯
{\displaystyle {\overline {CF}}}
A
D
¯
{\displaystyle {\overline {AD}}}
B
C
F
{\displaystyle BCF}
B
D
A
{\displaystyle BDA}
∠
C
A
B
{\displaystyle \angle CAB}
∠
B
A
G
{\displaystyle \angle BAG}
C
{\displaystyle C}
A
{\displaystyle A}
G
{\displaystyle G}
B
{\displaystyle B}
A
{\displaystyle A}
H
{\displaystyle H}
∠
C
B
D
{\displaystyle \angle CBD}
∠
F
B
A
{\displaystyle \angle FBA}
∠
A
B
D
{\displaystyle \angle ABD}
∠
F
B
C
{\displaystyle \angle FBC}
因為
A
B
¯
{\displaystyle {\overline {AB}}}
B
D
¯
{\displaystyle {\overline {BD}}}
F
B
¯
{\displaystyle {\overline {FB}}}
B
C
¯
{\displaystyle {\overline {BC}}}
△
A
B
D
{\displaystyle \triangle ABD}
△
F
B
C
{\displaystyle \triangle FBC}
因為
A
{\displaystyle A}
K
{\displaystyle K}
L
{\displaystyle L}
B
D
L
K
{\displaystyle BDLK}
△
A
B
D
{\displaystyle \triangle ABD}
因為
C
{\displaystyle C}
A
{\displaystyle A}
G
{\displaystyle G}
B
A
G
F
{\displaystyle BAGF}
△
F
B
C
{\displaystyle \triangle FBC}
因此四邊形
B
D
L
K
{\displaystyle BDLK}
B
A
G
F
{\displaystyle BAGF}
A
B
¯
2
{\displaystyle {\overline {AB}}^{2}}
同理可證,四邊形
C
K
L
E
{\displaystyle CKLE}
A
C
I
H
=
A
C
¯
2
{\displaystyle ACIH={\overline {AC}}^{2}}
把這兩個結果相加,
A
B
¯
2
+
A
C
¯
2
=
B
D
¯
×
B
K
¯
+
K
L
¯
×
K
C
¯
{\displaystyle {\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}}
由於
B
D
¯
=
K
L
¯
{\displaystyle {\overline {BD}}={\overline {KL}}}
B
D
¯
×
B
K
¯
+
K
L
¯
×
K
C
¯
=
B
D
¯
(
B
K
¯
+
K
C
¯
)
=
B
D
¯
×
B
C
¯
{\displaystyle {\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}={\overline {BD}}\left({\overline {BK}}+{\overline {KC}}\right)={\overline {BD}}\times {\overline {BC}}}
由於
C
B
D
E
{\displaystyle CBDE}
A
B
¯
2
+
A
C
¯
2
=
B
C
¯
2
{\displaystyle {\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}^{2}}
此證明是於歐幾里得 《幾何原本 》一書第1.47節所提出的[ 9]
由於這個定理的證明依賴於平行公理,而且從這個定理可以推出平行公理,很多人質疑平行公理是這個定理的必要條件,一直到十九世紀嘗試否定第五公理的非歐幾何 出現。
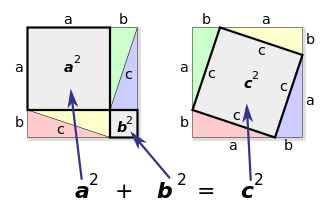
以面積減算法證明 此證明以圖形重新排列證明。兩個大正方形的面積皆為
(
a
+
b
)
2
{\displaystyle (a+b)^{2}}
a
2
+
b
2
{\displaystyle a^{2}+b^{2}}
c
2
{\displaystyle c^{2}}
以重新排列法證明
以動畫方式來論證畢氏定理 畢氏定理的逆定理是判斷三角形為鈍角、銳角或直角的一個簡單的方法,其中
A
B
¯
=
c
{\displaystyle {\overline {AB}}=c}
如果
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
△
A
B
C
{\displaystyle \triangle ABC}
∠
C
{\displaystyle \angle C}
如果
a
2
+
b
2
>
c
2
{\displaystyle a^{2}+b^{2}>c^{2}\,}
△
A
B
C
{\displaystyle \triangle ABC}
A
B
¯
=
c
{\displaystyle {\overline {AB}}=c}
∠
C
{\displaystyle \angle C}
如果
a
2
+
b
2
<
c
2
{\displaystyle a^{2}+b^{2}<c^{2}\,}
△
A
B
C
{\displaystyle \triangle ABC}
∠
C
{\displaystyle \angle C}
(這個逆定理其實只是餘弦定理 的一個延伸)
畢氏定理的逆定理的證法數明顯少於畢氏定理的證法。以下是一些常見證法。
構造
△
A
′
B
′
C
′
{\displaystyle \triangle A'B'C'}
a
′
=
a
,
b
′
=
b
,
∠
C
′
=
90
∘
{\displaystyle a'=a,b'=b,\angle C'=90^{\circ }}
根據畢氏定理,
c
′
=
a
′
2
+
b
′
2
=
a
2
+
b
2
=
c
{\displaystyle c'={\sqrt {a'^{2}+b'^{2}}}={\sqrt {a^{2}+b^{2}}}=c}
△
A
′
B
′
C
′
≅
△
A
B
C
(
S
S
S
)
{\displaystyle \triangle A'B'C'\cong \triangle ABC(SSS)}
因此,
∠
C
=
90
∘
{\displaystyle \angle C=90^{\circ }}
根據餘弦定理,
cos
C
=
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
cos
C
=
0
{\displaystyle \cos C=0\,}
∠
C
=
90
∘
{\displaystyle \angle C=90^{\circ }}
在
A
B
¯
{\displaystyle {\overline {AB}}}
D
{\displaystyle D}
∠
D
C
B
=
∠
A
{\displaystyle \angle DCB=\angle A}
在
△
C
D
B
{\displaystyle \triangle CDB\,}
△
A
C
B
{\displaystyle \triangle ACB\,}
∠
B
=
∠
B
,
∠
D
C
B
=
∠
A
⇒
△
C
D
B
∼
△
A
C
B
{\displaystyle \angle B=\angle B,\angle DCB=\angle A\Rightarrow \triangle CDB\sim \triangle ACB}
。
從而,
B
C
¯
B
A
¯
=
B
D
¯
B
C
¯
⇒
B
D
¯
=
a
2
c
{\displaystyle {\frac {\overline {BC}}{\overline {BA}}}={\frac {\overline {BD}}{\overline {BC}}}\Rightarrow {\overline {BD}}={\frac {a^{2}}{c}}}
C
D
¯
A
C
¯
=
C
B
¯
A
B
¯
⇒
C
D
¯
=
a
b
¯
c
{\displaystyle {\frac {\overline {CD}}{\overline {AC}}}={\frac {\overline {CB}}{\overline {AB}}}\Rightarrow {\overline {CD}}={\frac {\overline {ab}}{c}}}
另一方面,
A
D
¯
=
A
B
¯
−
B
D
¯
=
c
−
a
2
c
=
b
2
c
{\displaystyle {\overline {AD}}={\overline {AB}}-{\overline {BD}}=c-{\frac {a^{2}}{c}}={\frac {b^{2}}{c}}}
D
C
¯
A
D
¯
=
B
C
¯
A
C
¯
=
B
D
¯
C
D
¯
=
a
b
{\displaystyle {\frac {\overline {DC}}{\overline {AD}}}={\frac {\overline {BC}}{\overline {AC}}}={\frac {\overline {BD}}{\overline {CD}}}={\frac {a}{b}}}
△
A
C
D
∼
△
C
B
D
{\displaystyle \triangle ACD\sim \triangle CBD}
因而,
∠
B
D
C
=
∠
C
D
A
=
90
∘
{\displaystyle \angle BDC=\angle CDA=90^{\circ }}
∠
A
C
B
=
∠
C
D
B
=
90
∘
{\displaystyle \angle ACB=\angle CDB=90^{\circ }}
畢氏定理是由歐幾里得幾何 的公理推導出來的,其在非歐幾里得幾何中不成立的[ 10] 平行公設 。[ 11] [ 12]