යාගි–උඩා ඇන්ටෙනා

යාගි අඳින - උඩ අති උච්ච සංඛ්යාත රූපවාහිනී ඇන්ටනා 4, 54 - - 72 MHz (ඇමරිකා එක්සත් ජනපදය නාලිකා) ඇනලොග් නාලිකා 2 සඳහා භාවිතා 1954 සිට,. එහි මූලද්රව්ය පහක් ඇත: අධ්යක්ෂකවරු තිදෙනෙක් ( වමේ සිට ) එක් පරාවර්තකයක් ( දකුණට ) සහ දිශාභිමුඛ ( ඩයිපෝල් )   Ω twin ඊයම් පෝෂණය. කදම්භ දිශාව (ඉහළම සංවේදීතාවයේ දිශාව) වමට.

නවීන ඉහළ ලාභයක් UHF යාගි රූපවාහිනී ඇන්ටනා ලෙස හැඩ 17 අධ්යක්ෂවරුන්, සහ එක් පරාවර්තකය (පොලු 4 සාදා) සමග පරාවර්තී .

ආචරණ ගුවන් විදුලි නාලිකාවක් විසින් කෙටි දුර පෝලිම් වල දිගු දුරක් ( අහසෙහි ) සංනිෙව්දනය සඳහා භාවිතා කරන ලද ත්රිරෝද රථ Yagi - Uda ඇන්ටනා භාවිතා කරන ලදී. දිගු පරාවර්තක මූලද්රව්යය ( වමේ ), ධාවනය වන මූලද්රව්යය ( මධ්ය ) සහ කෙටි අධ්යක්ෂක ( දකුණේ ) එකිනෙකට සම්බන්ධ වන පරිදි ඊයම් උගුල (එකිනෙකට සමාන්තර LC පරිපථයක් ) ඒවායේ සන්නායකයන් එක් එක් පැත්තට ඇතුලත්ව ඇත. එක් සංඛ්යාත කලාපයකට වඩා.

ඒ යාගි - සාමාන්යයෙන් යාගි ඇන්ටනාව ලෙස උඩා ඇන්ටනාව,, යනු දිශාව ඇන්ටනාව රේඛාවක් දී බහු සමාන්තර අංග සමන්විත, සාමාන්යයෙන් අර්ධ තරංග dipoles ලෝහ පොලු සාදා. යාගි - උඩා ඇන්ටනා සම්ෙපේෂක ෙහෝ ග්රාහකයට සම්ෙපේෂකයට ෙහෝ සම්ෙපේෂණයට සම්බන්ධ ෙනොවන අතිෙර්ක පරෙපෝෂිත මූලදව්ය සමඟ සම්ෙපේෂකයකු ෙහෝ ලබන්නාට සම්බන්ධ වූ තනි උපකරණයක් අඩංගු ෙව්: ඊනියා පරාවර්තකයෙකි සහ එක් අධ්යක්ෂකවරයකු ෙහෝ වැඩි ගණනක්. එය 1926 දී ජපානයේ ටොහෝකු ඉම්පීරියල් විශ්ව විද්යාලයේ ෂින්ටාරෝ උඩු විසින් සහ (ඔහුගේ සගයා විසින් ඉටු කරන ලද අඩු භූමිකාවක් සමග) හයිටෙචුගි යාගි විසින් නිර්මාණය කරන ලදී .

පරාවර්තක ආලේපනය මෙහෙයවූ ඩිපෝල්ට වඩා තරමක් දිගු වන අතර අධ්යක්ෂවරු ටිකක් කෙටි වේ. පරපෝෂිත අංග වෙනස් සමග අවශෝෂණය හා පැදවූ අංගයක් සිට ගුවන් විදුලි තරංග විකිරණය අදියර වන ඩයිපෝල් ගේ කිරීමෙන්, විකරණය කිරීමෙන් විකිරණ රටාව . විවිධ බලවේග සිට තරංග superpose සහ මැදිහත් වන ඇන්ටනා ගණන්වල ඉතා සැලකිය යුතු වර්ධනයක් කරා, තනි දිශාවට විකිරණ වැඩි දියුණු කිරීම සඳහා ලාභ සරල dipole සාපේක්ෂව.

"කදම්බ ඇන්ටනා" ලෙසද හැඳින්වේ. හෝ "පරපෝෂිත අරා" ලෙස හැඳින්වේ. යාගි HF , VHF සහ UHF බෑන්ඩ්ස් හි ඉහළ ප්රතිදාන ඇන්ටෙනාවක් ලෙස බොහෝ ලෙස භාවිතා වේ. එය ඉහළ මට්ටමක් දක්වා ඇත වාසියක් සාමාන්යයෙන් 20 ක් පමණ සීමා භාවිතා අංග ගණන මත පදනම් වන,   dBi , රේඛීය ධ්රැවිකරණ , දිශාති්රක (අවසාන ආලෝකය ) කදම්බ රටාව ඉහළ ප්රතිවිරුද්ධ අනුපාතය 20   db. එය සැහැල්ලු, මිළ අඩුයි හා සරලයි. මෙම කලාප පළලක් ඇති යාගි ඇන්ටනාව, එම වාර ගණන එය ඉහළ ලාභයක් ඇති අධික පරාසය, මධ්ය සංඛ්යාතය සියයට කිහිපයක් පටු වන අතර, වැඩි වාසි සමඟ අඩු, එසේ ස්ථාවර සංඛ්යාත අයදුම්පත් එය බොහෝ විට භාවිතා කරනු . විශාලතම හා වඩාත්ම ප්රසිද්ධ භාවිතා වන්නේ භූමිෂ්ඨ රූපවාහිනී ඇන්ටනා ලෙසය. නමුත් එය ලක්ෂ්ය-ලක්ෂ්ය ස්ථාවර සන්නිවේදන සබඳතා සඳහාද රේඩාර් ඇන්ටනා සහ දුරස්ථ කෙටි දුර සන්නිවේදන සඳහා කෙටි විකාශන මධ්යස්ථාන සහ ගුවන් විදුලි නාලිකා.

මූලාරම්භය

මෙම ඇන්ටෙනා විසින් 1926 දී නිර්මාණය කළ ෂින්ටාරෝ උඩ ක ටොහෝකු ඉම්පීරියල් විශ්ව විද්යාලයේ , ජපානය , , ඔහුගේ සහායක විසින් ඉටු අඩු භූමිකාව සමග Hidetsugu Yagi .

කෙසේ වුවද "යාගි" නම ඌඩා බොහෝ විට අතහැර දමා ඇත. මෙම යාගි හි යූඩීගේ නම නොමැතිව යාගි පේටන්ට් බලපත්රයක් ලබා ගැනීමෙන් පසු, පේටන්ට් බලපත්රය එක්සත් රාජධානියේ මාර්කොනි සමාගමට පේටන්ට් බලපත්රය මාරු කර යැවීමට හේතු වී තිබේ.

බි්රතාන්ය, එක්සත් ජනපද, ජර්මානුවන් සහ ජපන් ජාතිකයන් විසින් රේඩාර් පද්ධතීන්හි දෙවන ලෝක යුධ සමයේදී ප්රථමයෙන් යාගි ඇන්ටනා භාවිතා කරනු ලැබීය. යුද්ධය අවසන් වීමෙන් පසු ඔවුන් රූපවාහිනී ඇන්ටනා ලෙස පුළුල් සංවර්ධනයක් දක්නට ලැබිණි.

විස්තර

Yagi - Uda ආලෝකය පරාවර්තක ( වමේ ), අර්ධ තරංග තරංග ක්රියාකාරී මූලද්රව්යය ( මධ්ය ) සහ අධ්යක්ෂ ( දකුණ ). නිශ්චිත මෝස්තර අනුව අනුවර්තනය කිරීම හා මූලද්රව්ය දිග ප්රමාණය නිශ්චිතව වෙනස් වේ.

Yagi - Uda ඇන්ටනා රේඛාව තුල සමාන්තර ටැන්ජ් පෝඩ් වර්ග ගණනාවක් අතර, සාමාන්යයෙන් අර්ධ තරංග තරංගයක්, සාමාන්යයෙන් සිය මධ්යස්ථාන ඔස්සේ විෂ්කම්භය හරස් අතට හෝ "උත්පාතය" මත රදවා ඇත. කේන්ද්රීයව මෙහෙයවන තනි ධාවන මූලද්රව්යයක් (සම්ප්රේෂිත මාර්ගයේ එක් පැත්තකින් එකිනෙකට සම්බන්ධ වන පොලු දෙකක්) සහ පරපුටු මූලද්රව්ය විචල්ය ගණනක්, එක් පැත්තක තනි පරාවර්තකයක් සහ විකල්ප වශයෙන් එක් පැත්තක හෝ තවත් අධ්යක්ෂකයකු හෝ . පරෙපෝෂිත මූලද්රව්ය සම්ප්රේෂකය හෝ ග්රාහකයාට විද්යුත් සම්බන්ධතාවයක් නොමැති අතර, විකිරණ රටාව වෙනස් කිරීම සඳහා රේඩියෝ තරංග රේඩියේටර් ලෙස ක්රියා කරයි . අංග අතර සාමාන්ය spacings නිශ්චිත සැලසුම් මත පදනම්ව, එහි තරංග ආයාමය ¼ කටත් ක් පමණ සිට වෙනස් වේ. අධ්යක්ෂකවරුන් විසින් මෙහෙයවන ලද මූලද්රව්යයට වඩා තරමක් කෙටි වන අතර පරාවර්තකය (s) තරමක් දිගු වේ. විකිරණ ආකෘතිය එක් දිශානුසාරීය වන අතර, අධ්යක්ෂකවරුන් සමඟ අවසානයෙහි මූලද්රව්යවල තලය තුළ මූලද්රව්යවල මූලිකව අක්ෂයේ දිශාවට අක්ෂය දිගේ ප්රධාන කවචය වේ.

සුවපහසු, එම dipole පරපෝෂිත අංග ඇති node එකක් මතම ඊට අදාල (ශුන්ය ලක්ෂ්යය RF වෝල්ටීයතා ඔවුන්ගේ මධ්යස්ථානය), ඒ නිසා ඔවුන් ඔවුන්ගේ විදුලි මෙහෙයුම් බාධා තොරව, පරිවාරක අවශ්ය තොරව එම අවස්ථාවේ දී එය සන්නායක ලෝහ සහාය අනුයුක්ත කල හැක. සාමාන්යයෙන් ඒවා ඇන්ටනාහි මධ්යම ආධාරක උත්ශ්රේණිගත කිරීම සඳහා සාමාන්යයෙන් සවි කර ඇති හෝ වෑල්වනය කරති. එහි ප්රධාන අංගය කේන්ද්රීයව පෝෂණය වන අතර එහි භාජන දෙපැත්තට ඒවායේ ආධාරය සඳහා අවශ්ය වන පරිදි පරිවරණය කළ යුතුය.

භාවිතා වන පරපෝෂිත මූලද්රව්ය සමඟ වැඩි වීම වැඩි වේ. අතිරේක පරාවර්තකයින්ගේ වැඩිදියුණු වීමක් ඇතිව වැඩිදියුණු කිරීම නිසා එක් පරාවර්තකයක් භාවිතා කරනු ලැබේ. එහෙත් Yagis 30 - 40 අධ්යක්ෂකවරුන් සමඟ ඉදිකර ඇත.

ඇන්ටෙනාවෙහි පළල කලාපය යනු ලාභය පහළ බැස ඇති සංඛ්යාතයන් අතර සංඛ්යාත පරාසය වේ   dB (එක් අර්ධ බලයක්) එහි උපරිමයට වඩා අඩුය. Yagi - Uda මාලාව එහි මූලික ආකෘතියේ ඉතා පටු තරංග පරාසයක් ඇති අතර කේන්ද්රීය සංඛ්යාතයෙන් 2 ත් 3 ත් අතර වේ. වාසි හා කලාප පළල අතර වෙළඳාමක් පවතී, වැඩි මූලද්රව්ය භාවිතා කරන විට කලාප පළල පටු වීම සමග. පෘථිවි රූපවාහිනිය වැනි පුළුල් කලාප පළල සඳහා අවශ්ය වන යෙදුම් සඳහා Yagi - Uda ඇන්ටනා සාමාන්යයෙන් VHF සහ UHF බෑන්ඩ්වල අදාල කොටස් ආවරණය කිරීම සඳහා ත්රිකෝණාකාර පිළිබිඹුවන් සහ විශාල විෂ්කම්භය කොන්දෙසර යොදා ගනී. පහත විස්තර කර ඇති පරිදි "උගුල්" භාවිතය මගින් පුළුල් කලාප පළලක් ලබා ගත හැකිය.

Yagi - Uda ඇන්ටනා ආධුනික ගුවන්විදුලි සඳහා සමහර බෑන්ඩ්ස් මත ක්රියාත්මක කිරීමට නිර්මාණය කර ඇත. මෙම විස්තීර්ණ මෝස්තර එක් එක් මූලද්රව්යය දෙපස විද්යුත් විවීමක් නිර්මාණය කරයි. එහිදී ලක්ෂ්ය LC ( ප්රේරක හා ධාරිත්රක ) පරිපථය ඇතුළත් වේ. මෙම ඊනියා උගුලට වැඩි සංඛ්යාත කලාපයේ මූලද්රව්යය කාවැදී ඇති අතර එහි දිග අඩි තරංග ආයාමයක් සෑදීමේ හැකියාව ඇත. අඩු සංඛ්යාතයකදී, සම්පූර්ණ අංගය (උගුලට හේතු වන ඉතිරි ප්රේක්ෂකය ඇතුලුව) අර්ධ තරංග තරංග අනුනාදණයට සමීපව වෙනස් Yagi - Uda ඇන්ටෙනාවක් ක්රියාත්මක කරයි. උගුල් දෙවන කට්ටලයක් භාවිතා කරමින්, ගෝත්රික ඇන්ටෙනාවක් එකිනෙකට වෙනස් කණ්ඩායම් තුනකට අනුකූල විය හැක. කුළුණකට ඉහලින් ඇන්ටෙනා හා රොටර් පද්ධති සවි කිරීම සඳහා අදාල පිරිවැය නිසා එක් ඒකකයක් තුළ ආධුනික බෑන්ඩ් තුනක් සඳහා ඇන්ටනා සංයෝග ඉතා ප්රායෝගික විසඳුමක් වේ. කෙසේ වෙතත්, උගුල් භාවිතා කිරීම, අවාසි නොමැතිව වුවද, එක් එක් පරාසයේ ඇති තරංගවල පළල අඩු කිරීම සහ ඇන්ටනාහි විද්යුත් කාර්යක්ෂමතාව අඩු කිරීම සහ අමතර යාන්ත්රික සලකා බැලීම් (සුළඟ නැව්ගත කිරීම, ජලය හා කෘමි ආක්රමණ) වලට ඇන්ටනා යටත් කිරීමයි.

මෙහෙයුමේ න්යාය

144 දී භාවිතා කළ හැකි ජංගම Yagi - Uda ඇන්ටෙනා   MHz (2   m), පැදවූ සහ පරපුටු මූලද්රව්යවල ආයුධ සඳහා කහ පටිය මැනීමේ පීත්ත පටිය සමග.

Yagi - Uda මෙහි දැක්වෙන්නේ පරාවර්තකය, මෙහෙයවන අංගය සහ තනි අධ්යක්ෂවරයෙකුගෙන් සමන්විත ය. මෙහෙයවන මූලද්රව්යය සාමාන්යයෙන් ½ කි <span typeof="mw:Entity" id="mwkw"> </span> <i id="mwlA">λ</i> dipole හෝ නවනු dipole සහ සෘජුව කලබල (වෙත, විද්යුත් වශයෙන් සම්බන්ධ බව ව්යුහය එකම සාමාජිකයෙකු වන feedline ). අනෙක් මූලද්රව්ය පරපුටු ලෙස සලකනු ලැබේ. එනම්, ඔවුන් මෙහෙයවනු ලබන මූලද්රව්යයෙන් ඔවුන් ලබා ගන්නා බලය ප්රතික්රියා කරති (ඔවුන් එකිනෙකා සමඟ අන්තර්ක්රියා කිරීම).

එවැනි ඇන්ටෙනාවක් ක්රියාත්මක කිරීම ගැන සිතීම එක් පරපෝෂිත මූලද්රව්යයක් එහි ධූමස්ථානය හරහා කෙටි පරිපථයක් සහිතව එහි මධ්යයේ දී පරිපථයේ විෂ්කම්භය සාමාන්ය සම්පීඩකයක් ලෙස සැලකිය යුතුය. සම්ප්රේෂිත මාර්ග සිද්ධාන්තය පිළිබඳ හොඳින් දන්නා පරිදි, කෙටි පරිපථය, අදියරෙන් අංශක 180 ක පමණ අංශකයක් මඟින් පිළිබිඹු වේ. එබැවින් පරපුටු මූල ද්රව්යයේ ක්රියාකාරිත්වය මැනිය හැකි ලෙස ඩිපෝල් මූලද්රව්යයේ සුපිරි ධ්රැවය ලෙස සම්ෙපේෂණය කරන ලද සම්ප්රේෂණ රේඛාවක් පහළට යැවීම හා සම්පේ්රෂණ මාර්ගය ඔස්සේ ඇන්ටෙනාව දෙසට සම්පේ්රෂනය වන සම්ප්රේෂණය කිරීම සඳහා සම්ප්රේෂකය මූලද්රව්යය. සම්ප්රේෂිත වෝල්ටීයතා තරංග 180 ක් නම්   එම ස්ථානයේ ලැබුණු තරංගය සමග අංශුවලින් බැහැරව ඇති අතර, වෝල්ටීයතා තරංගවල සුපිරි පිහිටීම, ශුන්ය වෝල්ටීයතාවයක් ලබා දෙනු ඇත. එය ප්රෝටීන් අගය (dipole) පිටතට ගැනීම සඳහා සමාන වේ. එබැවින් අර්ධ තරංග පරපුටු මූලද්රව්යය ආක්රමණ තරංගය සමඟින් 180 ° ක තරංගයක් විකාශනය කරයි.

පරපෝෂිත මූලද්රව්යය සම්බන්ධ වීම හරියටම අනුනාදයක් නොවන නමුත් ½ ට වඩා තරමක් කෙටි (හෝ වැඩි)   λ මූලයේ මූලද්රව්යයේ උච්චාවචනය සම්බන්ධයෙන් මූලද්රව්යයේ ධාරාවෙහි අදියර වෙනස් වේ. ඊනියා පරාවර්තක මූලද්රව්යය, ½ ට වඩා දිගු වීම   λ   , ක උද්ගාමී ඇත ප්රතිබාධනය එහි වත්මන් අවධිය ලැබුණු ක්ෂේත්රයේ අවිධිමත් බව විවෘත-පරිපථ වෝල්ටීයතා අවධිය lags, ඉන් අදහස් වන්නේ. අනෙක් අතට, අධ්යක්ෂවරයාගේ මූලධර්මය වන්නේ ½ ට වඩා අඩු වීමයි   λ   , වෝල්ටීයතා මට්ටමේ ධාරාව ඇතිව ධාරිතාවය සහිත ධාරිතක ප්රතිබාධයක් ඇත.

මූලද්රව්යවල නිවැරදි දිග හා විචල්යතාවයන් ලබා දී ඇති අතර, පරාමිතික මූලද්රව්ය මගින් නැවත විකිරණය වූ විකිරණ මගින් තරංග ආලෝක තරංග ආලෝකය තරංග ආයාම මඟින් අසමසම ඇනෑනියේ ඉදිරිපසට පැමිනේ. එබැවින් ඒවා සංවේදී හා සංඥා ශක්තිය වැඩි කිරීම, ඉදිරි දිශාව. වෙනත් වචනවලින් කිවහොත්, පරාවර්තක මූලද්රව්යයේ ඉදිරිපස තරංගයේ මූලාරම්භය, එම මූලද්රව්යයෙන් තරංගය මුදාහරිනු ලැබීම හරියටම ප්රත්යාවර්ත මූලද්රව්යයට ළඟා වේ. මෙම තරංගයේ මූලාරම්භක මූලද්රව්යය වෙතට මෙම රැළි ඇල්ලීම සිදු වේ. ප්රතිවිරුද්ධ දිශාවන්හි තරංගය විනාශකාරී ලෙස මැදිහත් වන අතර , අවලංගු වන නිසා, ප්රතිවිරුද්ධ දිශාවට විකිරණ සංඥා ශක්තිය කුඩා වේ. මෙලෙස ඇන්ටනාව අන්තේන්ද්රයේ රේඩියෝ තරංග (තනි අධ්යක්ෂක කදම්භයක්) රේඩියෝවෙන් (අධ්යක්ෂ අධ්යක්ෂණය) විකිරණනය කරයි.

විශ්ලේෂණය

පරපුටු මූලද්රව්ය එකිනෙකට වැය වන වියදමෙන් එක් දිශාවකින් සිදුවන විකිරණ මූලද්රව්ය වැඩිදියුණු කළ හැකි බව ඉහත ගුණාත්මක පැහැදිලි කිරීම ප්රයෝජනවත් වන අතර, භාවිතා කරන උපකල්පන ඉතා නිවැරදියි. දිගු පරපෝෂිත මූලද්රව්යය වන දිගු පරපුටු මූල ද්රව්යය නිසා, මෙහෙයවන ලද මූලද්රව්යයේ තාපය අඩු වී ඇති නිසා, යගයි - යූඩා ඇන්ටෙනාවේ සැබෑ දිශාව ට පටහැනිව ප්රතිබිම්බයෙහි දිශාවෙහි දිශාව පෙන්වීමට අපේක්ෂා කරයි . ඇත්ත වශයෙන්ම, එය සිදුවන්නේ නම්, අප විසින් ඉදිරිපත් කරන ලද පරිපථවල දිශාගතව ඇති වෝල්ටීයතාවන් විසින් ධාවනය කරනු ලබන තරමක් පරමාණුක වස්තූන් සහිත ව්යුත්පන්න ආවාටයක් නිර්මාණය කිරීමයි.

කෙසේ වෙතත් මෙම මූලද්රව්ය ලෙස මෙහෙයවනු නොලැබුවද, මෙහෙයවන ලද මූලද්රව්ය මගින් නිර්මාණය කරන ලද ක්ෂේත්රයෙන් ඔවුන්ගේ ශක්තිය ලබා ගනී. එබැවින් අපට සත්යය විය හැකි ප්රතිවිරුද්ධයයි. දැන්, පැරසිටික් මූලද්රව්යයේ දිග ද λ / 2 ට සමාන බව සලකන්න. පරපෝෂිත මූලද්රව්යයේ පරපෝෂිත මූලද්රව්යය දිගේම දිග්ලෑවක් ලෙස සැලකෙන පරපෝෂිත මූලද්රව්යයක් ලෙස ක්රියා කරන ලද මූලද්රව්යයට ප්රතිචාර දැක්වීමෙන් ආරම්භ කරන ලද මූලද්රව්යයට සම්බන්ධ වන විවෘත පරිපථයේ ප්රොටොපොම්පේ වෝල්ටීයතාවයට ප්රතිචාර දැක්විය හැකි බව අපට දැකිය හැකිය. අපි දැන් උපකල්පනය කරමු) එවිට කෙටි පරිපථයේ ඇති පරාවර්තක තරංගය මෙහෙයවනු ලබන මූලද්රව්යයේ ධාරාව සමඟ ධාරාවකින් 180 ° ක් අක්රියවනු ඇත. මෙය මෙහෙයවනු ලබන මූලද්රව්ය විකිරණය අවලංගු කිරීමට නැඹුරු වේ. කෙසේ වෙතත්, දිග වෙනස් වීමෙන් ඇතිවන ප්රතික්රියාකාරිත්වය නිසා, පරාවර්තකයේ ධාරාවෙහි ඇතිවන තත්පරයට සාපේක්ෂව 180 ° පසුබෑමකට හේතු වේ. එහි ප්රතිඵලයක් වශයෙන් අධ්යක්ෂක වරයාට ඉදිරි පියවරක් ඇති වේ. එබැවින් අරාවෙහි සෘජුකාරකත්වය ඇත්ත වශයෙන්ම අධ්යක්ෂක වෙත යොමු වී තිබේ.

• 
  ඇන්ටනාව ක්රියා කරන්නේ කෙසේද? සෑම මූලද්රව්යයකම රේඩියෝ තරංග නිකුත් කරනුයේ එක් පියවරක් ප්රමාද වීමෙනි. එබැවින් ඉදිරි දිශාව (ඉහළ) තුළ නිකුත් කරන තනි තරංගවල ප්රතික්රියා අතර වේ. ඒ නිසා, ඉදිරි තරංග එකට (එකතු කරන්න, නිර්මාණාත්මක නිරෝධනය ) ඒ දෙසට බලය ශක්තිමත් කරමින් මෙම පසුගාමී තරංග අර්ධ වශයෙන් එකිනෙකාට (අවලංගු අතර විනාශකාරී බලපෑම් එමගින් එම දිශාවට විමෝචනය බලය අවම කිරීම,). අනෙක් කෝණ වලදී, විමෝචනය වන බලය අන්ත දෙක අතර අතරමැදි වේ.
• 
  යගයි - යූඩා ආයි්රේ දෙකක (වාමාංශික) සහ අධ්යක්ෂ (දකුණේ) පමනක් යොදා ගනිමින් ඉලක්කම් දෙකක ඉදිරි වර්ධනයක් නිරූපනය කිරීම. රියදුරු මූලද්රව්යයෙන් (රතු) තරංගය (හරිත) කිසියම් අවධියක මාරු කරන නිල් (රතු) තරංගයක් රදාපවතින අතර එය (පාඨයේ පැහැදිලි කිරීම බලන්න) බලන්න. මෙම තරංගයේ එකතු (පහළ) ඉදිරි දිශාවෙහි වැඩි වන නමුත් ආපසු හැරීම මඟහරවා ගත හැකිය.
• 
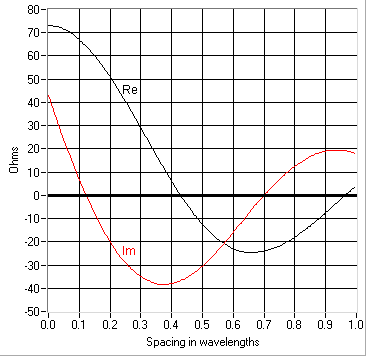
  සමාන්තර අතර අන්යෝන්ය සම්බාධනය ව්‍යාකරණ විග්‍රහය අසමත් විය (කාරක-රීති දෝෂය): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><mrow class="MJX-TeXAtom-ORD"><mfrac><mi> <math>\scriptstyle{{\lambda \over 2}}} </mi><mn> $\scriptstyle {\lambda \over 2}$ </mn></mfrac></mrow></mrow> </math>$\scriptstyle {\lambda \over 2}$ $\scriptstyle {\lambda \over 2}$ ඩයිපයිස් නොගැලපෙන පරිදි විහිදෙන කාර්යයක් නොවේ. Curves Re සහ Im යනු ප්රතිරෝධීය සහ ප්රතික්රියාකාරක අන්යෝන්ය සම්බාධනයයි. ශුන්ය පරතරයක් ඇති විට අපි අර්ධ තරංග තරංග ඩිප්ලෝල් ස්වයං සම්බාධනය ලබා ගනිමු   +   j43   Ω.

අධ්යක්ෂවරුන් හා පරාවර්තක (s) යන දෙඅංශයේ පවත්නා ධාරාවන්ගේ අදියර තවදුරටත් ප්රමාද වන මූලද්රව්ය අතර සීමිත දුර ප්රමාණය හේතුවෙන් අතිරේක පියවර ප්රමාදයක් සැලකිල්ලට ගත යුතුය. Yagi - Uda මාලාවක් භාවිතා කරන ලද යතුරු පුවරුවක සහ අධ්යක්ෂකවරයෙකු යොදාගෙන ඇති අතර මෙම සියලු ප්රතිඵල සැලකිල්ලට ගනිමින් මෙම රූප සටහනෙහි නිදර්ශනය කර ඇත. පාලිත මූලද්රව්යය විසින් උත්පාදනය කරන ලද තරංගය (හරිත) ඉදිරියට සහ ආපසු හරවන දිශාවන් දෙකම (සහ වෙනත් දිශාවන් නොපෙන්වන) පැතිරෙයි. අධ්යක්ෂවරයාට ලැබෙන්නේ එම කාල වකවානුවේදී (පසුකාලීන දිශාව ගණනය කිරීම් සඳහා වැදගත් වනු ඇති 35 ° ක අනුක්රමික ප්රමාදයක්) වන අතර, මෙහෙයවන ලද මූලද්රව්යය සමඟ අක්රිය වන ධාරාවක් උත්පාදනය කිරීම (එමගින් අතිරේක 180 ° අදියර මාරු කිරීම), නමුත් අධ්යක්ෂවරයාගේ කෙටි කාලය හේතුවෙන් අදියර (උෂ්ණත්වය 70 °) තවදුරටත් වැඩි දියුණු වේ. ඉදිරි දිශාව තුළ ශුද්ධ බලපෑම යනු මෙම නිශ්චිත සැලසුමේ දී රියදුරු මූලද්රව්යය (කොළ) සිට පාලනය වන 110 ° (180 ° - 70 °) පමණ වන අධ්යක්ෂක (නිල්) විසින් නිකුත් කරන තරංගයක් වේ. මෙම රැළි එකිනෙකට සම්බන්ධ වන තරංගවල (පහළ, දකුණට) තනි තරංගයක් මෙන් මදක් විශාලය.

අනෙක් අතට, අනෙක් අතට, දෙකේ අතර පරතරය හේතුවෙන් අධ්යක්ෂණය (නිල්) සිට රවුමේ අතිරේක ප්රමාදය (දෙවරක් ගමන් කර ඇති දිගු ප්රමාදය ප්රමාණයේ 35 ° ක් පමණ) එය 180 ° (110 °   +   2    ×   35 °) රියදුරු මූලද්රව්යය (හරිත) රැල්ල සමග අදියරයෙන් පිටත. මෙම දෙකේ රැළි (ශුද්ධ, වමේ) වල ඇති වූ ශුද්ධ බලපෑම් සම්පූර්ණයෙන්ම අවලංගු වේ. අධ්යක්ෂවරයාගේ පිහිටීම හා කෙටි කාලයෙහි සංයෝජනයක් නිසා ධ්රැවීය (අර්ධ තරංග තරංග ඩිපෝල්) මූලද්රව්යයේ තනි දෙආකාරකයක් පමණක් ලබා ගත හැකිය.

එවැනි ක්රමයක් පිළිබඳ සම්පූර්ණ විශ්ලේෂණය dipole අවයව අතර අන්යෝන්ය සම්බාධනය ගණනය අවශ්ය නිසැකයෙන්ම සැලකිල්ලට අවයව අතර පරිමිත පරතර ලෑම නිසා පැතිරවීම ප්රමාද කාලයක් ගතවේ. අපි වෝල්ටීයතා V _j හා ඒ තුළට ගලා යන ධාරාව I _j සමග මධ්යස්ථානයේ feedpoint සහිත අංගයක් අංකය j ආදර්ශයට. එවැනි මූලද්රව්ය දෙකක් සලකා බලමින් අපට එකිනෙකා අතර සම්බාධක Z _ij භාවිතා කරන ධාරාවන් අනුව,

ව්‍යාකරණ විග්‍රහය අසමත් විය (කාරක-රීති දෝෂය): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><msub><mi> <math> V_1 = Z_{11} I_1 + Z_{12} I_2 } </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mn></mrow></msub><mo> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mo><msub><mi> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mn></mrow></msub><msub><mi> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mn></mrow></msub><mo> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mo><msub><mi> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mn></mrow></msub><msub><mi> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </mn></mrow></msub></mrow> </math>$V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ $V_{1}=Z_{11}I_{1}+Z_{12}I_{2}$ </img>

ව්‍යාකරණ විග්‍රහය අසමත් විය (කාරක-රීති දෝෂය): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><msub><mi> <math> V_2 = Z_{21} I_1 + Z_{22} I_2 } </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><mo> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mo><msub><mi> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><msub><mi> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><mo> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mo><msub><mi> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><msub><mi> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub></mrow> </math>$V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ $V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </img>

Z ₁₁ සහ Z ₂₂ සාමාන්යයෙන් ඩයිපොල් වල සාමාන්ය ධ්රැව ධාරා සම්බාධන වේ   +   j43   අර්ධ රැල්ලේ මූලද්රව්ය සඳහා ඕම්ස් (සාමාන්යයෙන් අපේක්ෂිත මූලද්රව්යය සඳහා සාමාන්යයෙන් අපේක්ෂිත පරිදි හෝ තරමක් කෙටි වන හෝ හුදෙක් ප්රතිරෝධී). මූලද්රව්යයේ දිග වල Z ₁₁ සහ Z ₂₂ යන වෙනස්කම් සැලකිය යුතු ලෙස ප්රතික්රියාශීලී උපාංගයක් ඇත. සංහිඳියාව නිසා Z ₂₁ = Z ₁₂ අපි දන්නවා. දැන් අසීරු ගණනය කිරීම සංඛ්යාත්මක විසඳුමක් අවශ්ය වන අන්යෝන්ය සම්බාධනය Z ₂₁ තීරණය කිරීමයි. මෙම ප්රස්ථාරයේ ප්රස්ථාරයේ විවිධ දුරේක්ෂවලදී නිශ්චිත අර්ධ තරංග තරංග ඩයිපෝල් මූලද්රව්ය දෙකක් සඳහා මෙය ගණනය කර ඇත.

පද්ධතියේ විසඳුම පහත පරිදි වේ. එන්ජිම _{1 හි 1} සහ I ₁ ලෙස හැඳින්වෙන අතර එය සම්ප්රේෂකය මගින් සපයනු ලබන වෝල්ටීයතාව සහ ධාරාව වේ. පරපෝෂිත මූලද්රව්යය 2 ලෙස නම් කර ඇති අතර, එහි "feedpoint" හි කෙටි නිසා එය අපට V _{2 ලෙස} ලිවිය හැකිය   =   0. ඉහත සම්බන්ධතා භාවිතා කිරීමෙන්, මම _{1 1} සඳහා I ₂ සඳහා විසඳිය හැකිය:

ව්‍යාකරණ විග්‍රහය අසමත් විය (කාරක-රීති දෝෂය): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><mn> <math>0 = V_2 = Z_{21} I_1 + Z_{22} I_2 } </mn><mo> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mo><msub><mi> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><mo> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mo><msub><mi> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><msub><mi> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><mo> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mo><msub><mi> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub><msub><mi> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </mn></mrow></msub></mrow> </math>$0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ $0=V_{2}=Z_{21}I_{1}+Z_{22}I_{2}$ </img>

ඉතිං මොක ද

ව්‍යාකරණ විග්‍රහය අසමත් විය (කාරක-රීති දෝෂය): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><msub><mi> <math>I_2 = - {Z_{21} \over Z_{22}} \, I_1 } </mi><mrow class="MJX-TeXAtom-ORD"><mn> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mn></mrow></msub><mo> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mo><mo> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mo><mrow class="MJX-TeXAtom-ORD"><mfrac><msub><mi> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mn></mrow></msub><msub><mi> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mn></mrow></msub></mfrac></mrow><msub><mi> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </mn></mrow></msub></mrow> </math>$I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ $I_{2}=-{Z_{21} \over Z_{22}}\,I_{1}$ </img> .

මෙම පාලිත මූලද්රව්යයේ වර්තමාන I ₁ නිසා පරපෝෂිත මූලද්රව්යයෙහි ඇති ධාරාව මෙයයි. අපි මීට පෙර සමීකරණය භාවිතා කරමින් ධාවනය මූලද්රව්යයක feedpoint දී වෝල්ටීයතාව V ₁ විසඳීමට ද හැකි:

ව්‍යාකරණ විග්‍රහය අසමත් විය (කාරක-රීති දෝෂය): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><mrow class="MJX-TeXAtom-ORD"><mtable displaystyle="true" rowspacing="3pt"><mtr><mtd><msub><mi> <math>\begin{align} V_1 &= Z_{11} I_1 + Z_{12} I_2 = Z_{11} I_1 - Z_{12}{Z_{21} \over Z_{22}} \, I_1 \\ &= \left( Z_{11} - {Z_{21}^2 \over Z_{22}} \right) I_1 \end{align}} </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub></mtd><mtd><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><mrow class="MJX-TeXAtom-ORD"><mfrac><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub></mfrac></mrow><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub></mtd></mtr><mtr><mtd><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo><mrow><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo><mrow><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo><mrow class="MJX-TeXAtom-ORD"><mfrac><msubsup><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msubsup><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub></mfrac></mrow></mrow><mo> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mo></mrow><msub><mi> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </mn></mrow></msub></mtd></mtr></mtable></mrow></mrow> </math>${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ ${\begin{aligned}V_{1}&=Z_{11}I_{1}+Z_{12}I_{2}=Z_{11}I_{1}-Z_{12}{Z_{21} \over Z_{22}}\,I_{1}\\&=\left(Z_{11}-{Z_{21}^{2} \over Z_{22}}\right)I_{1}\end{aligned}}$ </img>

අපි Z ₁₂ = Z ₂₁ ආදේශ කළෙමු. මෙම ලක්ෂ්යයේදී වෝල්ටීයතාවයට අනුපාතය අනුපාතය 2-Eleg Yagi හි Z _dp වන ධාවක ලක්ෂයේ සම්බාධනයයි :

ව්‍යාකරණ විග්‍රහය අසමත් විය (කාරක-රීති දෝෂය): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><msub><mi> <math> Z_{dp}= V_1 / I_1 = Z_{11} - {Z_{21}^2 \over Z_{22}} } </mi><mrow class="MJX-TeXAtom-ORD"><mi> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mi><mi> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mi></mrow></msub><mo> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mo><msub><mi> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mn></mrow></msub><mrow class="MJX-TeXAtom-ORD"><mo> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mo></mrow><msub><mi> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mn></mrow></msub><mo> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mo><msub><mi> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mn></mrow></msub><mo> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mo><mrow class="MJX-TeXAtom-ORD"><mfrac><msubsup><mi> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mn></mrow><mrow class="MJX-TeXAtom-ORD"><mn> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mn></mrow></msubsup><msub><mi> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mi><mrow class="MJX-TeXAtom-ORD"><mn> $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </mn></mrow></msub></mfrac></mrow></mrow> </math>$Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ $Z_{dp}=V_{1}/I_{1}=Z_{11}-{Z_{21}^{2} \over Z_{22}}$ </img>

රියදුරු ලක්ෂ්යය සම්බාධනය පමණක් වන අතර, එය නිකම්ම Z _{11 වේ} , නමුත් පරපෝෂිත මූලද්රව්යය පැමිණීම මගින් දැන් වෙනස් කර ඇත. හා දැන් ඉහත ගණනය ලෙස මම ₁ සම්බන්ධයෙන් මම ₂ වන අදියර (සහ විස්තාරය) දැන හේතුවෙන් මෙම මූලද්රව්ය දෙක ගලන ධාරා සඳහා විකිරණ රටාව (දිශාව ශ්රිතයක් ලෙස වාසි) තීරණය කිරීම සඳහා අපට ඉඩ දී ඇත. අංග දෙකක් කට වඩා වැඩි එවැනි ඇන්ටනාව විසඳුමක් එක් එක් V _j ස්ථාපිත කරමින්, එම රැහැන් ඔස්සේ ඇදී යයි   =   පැදවූ අංගයක් නමුත් සියලු 0 අතර, එක් එක් අංගයක් දී දියවැල් (සහ වෝල්ටීයතාවය V ₁ feedpoint දී) ගතයුතුයි.

Yagi - Uda ඇන්ටනා තනි මාස්ටර් මත. ඉහළට කෙළවරේ පරාවර්තකයක් සහ කක්ෂය තුල තෙතමනය සහිත ධාරා තුනකින් සමන්විතය. තිරස් දිශාවට වැඩි වීම (බිම හෝ අහස දෙසට විකාශනය වන බලය අවලංගු කිරීම) සඳහා වැඩිදියුණු කරන ලදී. පහළ ඇන්ටෙනා වඩා අඩු අඩු අනුනාද සංඛ්යාතයක් සහිත සිරස් ධ්රැවාන්තකරණය සඳහා යොමු වී ඇත.

නිර්මාණ

භෞතික පරාමිතීන් අතර සංකීර්ණ සම්බන්ධතා නිසා Yagi - Uda ඇන්ටනා නිර්මාණය කිරීම සඳහා සරල සමීකරණයක් නොමැත

• මූලද්රව්ය දිග හා පරතරය
• මූල විෂ්කම්භය
• කාර්ය සාධන ලක්ෂණ: වාසි සහ ආදාන සම්බාධනය

කෙසේ වෙතත් ඉහත සඳහන් වර්ගීකරණ විචල්ය විශ්ලේෂණය භාවිතා කළ හැකි වන පරිදි පරාමිති කට්ටලයක් ලබා දෙන කාර්යසාධනය ගණනය කර ලාභය සඵල කර ගැනීම සඳහා ඒවා සකස් කිරීම (සමහර විට යම් සීමාවන්ට යටත්වේ). N Yagi - Uda antenna n නාලිකාව සමඟ 2 n   -   සැකසීමට පරාමිතීන් 1 (මූලද්රව්ය දිග හා සාපේක්ෂ දුරේක්ෂ). මෙම පසුබිමේ විශ්ලේෂණ ක්රමය සරල නොවේ. ඉහත සඳහන් කළ අන්යෝන්ය සම්බාධක පමණක් λ / 2 දිග මූලද්රව්යවලට අදාළ වන නිසා, ඒවා නිවැරදිව නිරවද්යතාව සඳහා නැවත සලකා බැලිය යුතුය.

සැබෑ ඇන්ටෙනා අංගයක් ඔස්සේ වත්මන් ව්යාප්තිය ආසන්න වශයෙන් ලබා දී ඇත්තේ සම්භාව්ය ස්ථාවර රැල්ලක සුපුරුදු උපකල්පනයෙනි. අනෙක් කොන්දොස්තරවරුන් සැලකිල්ලට ගනිමින් හලන්ගේ සම අනුකූල සමීකරණයට අවශ්ය වේ. ඉහත සදහන් සියළු අන්තර්ක්රියාකාරිත්වය සැලකිල්ලට ගෙන එවන් සම්පූර්ණ විශ්ලේෂණයක් විශ්ලේෂණය කිරීම අතිශයින්ම අතිමහත් ය. ප්රයෝජනවත් ඇන්ටෙනාවක් සොයා ගැනීමේ මාර්ගයේ ආසන්න වශයෙන් ආසන්න වශයෙන් අපරිමිත වේ.

මෙහි ප්රතිඵලයක් වශයෙන්, මෙම ඇන්ටනා බොහෝ විට අනුභූතික නිර්මාණයක් වන අතර අත්හදා බැලීමේ සහ දෝෂයක් සහිත අංගයකි, බොහෝ විට ආරම්භයේ පවතින මෝස්තරයට අනුව වෙනස් කර ඇත. ප්රතිඵලය සෘජු මිනුම් හෝ පරිගණක සිෙමන්ති මගින් සළකුණු කළ හැකිය.

මෙම පසුබිමෙහි භාවිතා වූ ප්රසිද්ධ මූලාශ්රයක් වන්නේ ජාතික ප්රමිති කාර්යාංශය (NBS) (දැන් ජාතික ප්රමිති හා තාක්ෂණ ආයතනය (NIST) විසින් නිකුත් කරන ලද වාර්තාවකි.   MHz සහ මෙම සැලසුම් වෙනත් සංඛ්යාතයන්ට අනුගත වීම සඳහා ක්රියා පටිපාටි. මෙම සැලසුම් සහ ඒවායේ ව්යුත්පන්නයන් සමහර විට හැඳින්වෙන්නේ "NBS yagis" ලෙසිනි.

යාබද අධ්යක්ෂවරුන් අතර දුර ප්රමාණය සකස් කිරීම මගින් විකිරණ රටාවෙහි පිටුපස කවුළුව අඩු කළ හැකිය.

ඉතිහාසය

Nahakima J1N 1-S රාත්රී සටන්කරුවෙකු සිව්පාවර් Yagi රේඩාර් සංවේදකය ඇන්ටනා

මෙම Yagi - උඩ ඇන්ටනාව විසින් 1926 දී නිර්මාණය කළ ෂින්ටාරෝ උඩ ක ටොහෝකු ඉම්පීරියල් විශ්ව විද්යාලයේ , සෙන්ඩායි , ජපානය සමග එක්ව, Hidetsugu Yagi ද ටොහෝකු ඉම්පීරියල් විශ්ව විද්යාලයේ. Yagi සහ Uda විසින් තරංග ප්රක්ෂේපණ යන්ත්රවල දිශා තරංග ආතන්නයේ මුල්ම වාර්තාව ප්රසිද්ධියට පත් කරන ලදී. යාගි සංකල්පයක් ඔප්පු කළ නමුත් ඉන්ජිනේරු ගැටලු සාම්ප්රදායික පද්ධතියට වඩා සංවේගයට පත් විය.

ජපානයේ කෙටි කාලීන පර්යේෂණ පිළිබඳව 1958 සමීක්ෂණ වාර්තාවේ දී පළ වූ ඉංග්රීසි භාෂාව පිළිබඳ පළමුවෙන් යාගි විසින් ඔහුගේ නමට සම්බන්ධ විය. කෙසේ වෙතත් Yagi සෑම විටම සැලසුම් කර ඇති Uda හි ප්රධාන දායකත්වය පිළිගත් අතර, ඇන්ටෙනාව සඳහා නිසි නම වන්නේ Yagi - Uda ඇන්ටෙනාව (හෝ අරා) ලෙසය.

ජර්මානු ෆුජී 220 රේඩාර් හි යාගි අරාවන් අග භාගයේ දෙවන ලෝක යුද්ධයේ මස්ටර්ෂිම්ට් 110 ප්රහාරක යානා.

යාදි ප්රථම වරට ගුවන් යානා රේඩාර් කට්ටල සඳහා දෙවන ලෝක යුධ සමයේදී භාවිතා කරනු ලැබුවේ එහි සරලත්වය සහ දිශානතිය නිසාය. ජපානය තුල නිපදවන ලද නමුත් ජපන් රේඩාර් ඉංජිනේරුවන් බොහෝ විට යුද්ධයේ දී ඉතා ප්රමාද වන තෙක් නිර්මාණයේ නොදැනුවත්බව, අර්ධ වශයෙන් යුධ හා නාවුක හමුදාවන් අතර ප්රතිවිරෝධතාව නිසා විය. ජපන් මිලිටරි බලධාරීන් ප්රථම වරට සිංගප්පූරුවේ සටනෙන් පසුව මෙම යගයි ඇන්ටෙනාව සඳහන් කළ බ්රිතාන්ය රේඩාර් කාර්මික ශිල්පියෙකුගේ සටහන් අල්ලා ගත් අවස්ථාවෙහි පළමුව දැන සිටියහ. මෙම සන්දර්භය තුළ යාගි ජපන් නමක් බව ජපාන බුද්ධි අංශ නිලධාරීන් පවා පිළිගත්තේ නැත. ජපන් මහාචාර්යවරයෙකු විසින් නම් කරන ලද ඇන්ටෙනාවක් යැයි ප්රශ්න කළ විට කාර්මික ශිල්පියෙකු පැවසුවේය.

ඒ තිරස් අතට කණ්ඩායම් දෙකකට අරා ප්රධාන අද්දර යටතේ දැක ගත හැකිය Grumman රජයට සහ Avenger ගුවන් මත පදනම් එක්සත් ජනපද නාවික හමුදාව ගුවන් යානා හා ඒකාබද්ධ PBY Catalina දිගු දුර මුර seaplane. වර්ථමානයේ දී ධ්රැවීකරණය කරන ලද අරා හි පී-61 හි කම්මුල් මත සහ WWII ගුවන් යානා බොහොමයක නාස් කොළ මත දක්නට ලැබේ. විශේෂයෙන් Lichtenstein රේඩාර් - ජර්මානු Junkers Ju 88 R-1 ප්රහාරක බෝම්බකරු සහ බි්රතාන්ය බ්රිස්ටල් බොයිෆයිටර් රාත්රිය සටන්කාමියෙක් සහ කෙටි සන්ඩර්ලන්ඩ් පියාසර කරන බෝට්ටුවක්. නාසය හා වලිගය දී, සහ සිතුවම් මුදුනේ එහි භයානක turreted ආරක්ෂක යුධෝපකරණ අමතරව - - ඇත්ත වශයෙන්ම, අග එහි නැවත සකස්කර බොහෝ ඇන්ටනාව බලවේග ප්රකාශ එය ජර්මානු ගුවන් භටයන් විසින් fliegendes Stachelschwein, හෝ "පියාසර ඉත්තෑවා" යන අන්වර්ථ නාමයෙන් කරන ලදී. 1943 - 44 සමීක්ෂණයේ ඇති Morgenstern ජර්මන් AI VHF-band රේඩාර් ඇන්ටනා විසින් එකිනෙකට වෙනස් ද්විමය ද්විත්ව මූලද්රව්ය හයක් නිර්මාණය කරන ලද Yagi ඇන්ටනා 90 ° යුගල සහිත Yagi ආකෘතියක් භාවිතා කළ අතර එමඟින් කොන්කීක්, රබර් ගුවන් යානා නාසය මත ප්ලයිවුඩ් රේඩෝව සඟවාගත් අතර, රේඩම්ගේ මතුපිට සිට Morgenstern හි ඇන්ටෙනා අංගවල අතිශය ඉඟි සහිතව, එහි එල්ටීටීඑස්ටේන් SN-2 සඳහා යුද්ධයේ අවසාන භාගයේ භාවිතා කරන ලද ගුවන් සේවයේ NJG 4 Ju 88 G-6 AI රේඩාර්.

දෙවන ලෝක සංග්රාමයෙන් පසුව රූපවාහිනී විකාශනය ඇරැඹීම, යාගි - යූඩා ඇන්ටෙනාහි වී.එෆ්.පී. සහ යූඑෆ්එෆ් බෑන්ඩ්ස් හි ක්වොපොප් රූපවාහිනී ඇන්ජිමේ ඇන්ටෙනා ලෙස හා එම්එම්එම් රේඩියෝ ඇන්ටෙනා තරමක් දුරට විය. මෙම සංවර්ධනය වන තුරු ලඝු-සටහන-ආවර්තිතා ඇන්ටෙනා 1960 දී, එය ප්රමාණවත් දිය හැකි ඇන්ටෙනා එකම වර්ගය විය වාටිය පිළිගැනීමේ දුර රූපවාහිනී සම්ප්රේෂකය සිට ප්රදේශවල. ප්රධාන පසුබෑමක් වූයේ යාගිගේ නෛසර්ගික පටු තරංග කලාපයයි. පුළුල් රූපවාහිනී පටි ඔස්සේ ප්රමාණවත් වාසියක් ලබා ගැනීම සඳහා ඉතා සංකීර්ණ යාගි නිර්මාණ දියුණු කරන ලදි. රූපවාහිනී ඇන්ටනා තවමත් Yagi ඇන්ටෙනාවේ ප්රධාන යෙදුමකි.

Yagi - Uda ඇන්ටනා 1995 දී IEEE Milestone ලෙස නම් කරන ලදී.

බලන්න

• ඇන්ටනා (ගුවන් විදුලි)
• ලැර්මර් සූත්රය
• ලොග්-පැ periodic dipole array
• සංඛ්යාත විද්යුත් විද්යුත් චුම්බක කේතය
• රේඩියෝ දිශාව සොයන්නා
• රේඩියෝ දිශාව සොයා ගැනීම

පරිශීලන

සයිට්ස්

ග්රන්ථ නාමාවලිය

• බ්රවුන්, ලුවිස් (1999). දෙවන ලෝක යුද්ධයේ රේඩාර් ඉතිහාසයක්: තාක්ෂණික හා මිලිටරිමය අවශ්යතාවයන් [1] . CRC මාධ්යය. ISBN 0-7503-0659-9 ISBN   0-7503-0659-9
• S. යුඩා, "කෙටි විදුලි තරංගවල අධි කෝණය විකිරණය". IRE හි කාර්යයන් , vol. 15, පි.   377 - 385 මැයි 1927.
• එස්ඩීඩා, "අර්ධ මීටර් තරංග මත විකිරණ රූපවාහිනිය සහ රේඩියෝotelephony". IRE හි කාර්යයන් , vol. 18, පි.   වර්ෂ 1930 ජුනි 1047 - 1063.
• එන්.ඊ. බ්රිටාන්, අතීතය පරික්ෂා කිරීම, ෂින්ටාරෝ යුඩා සහ වයිට් ප්රොජෙක්ටර්, ප්රෙස්. IEEE, මැයි 1997, pp.   800 - 801.
• එච්. යාගි, බීඩම් අධි-කෙටි තරංග සම්ප්රේෂණය , IRE හි කාර්යයන්, vol. 16, පි.   715 - 740, ජූනි 1928. මෙම URL එක 1997 වර්ෂයේදී සම්මත ග්රන්ථයක් වන IEEE නැවත මුද්රණය කිරීමයි. මෙයද බලන්න ක්ලැසික් කඩදාසි වන විට එච් Yagi සඳහා හැඳින්වීමක්: Ultra කෙටි තරංග කදම්බයක් සම්ප්රේෂණ දි.මු. Pozar විසින්, එක්ව IEEE වැඩ කටයුතු , වෙළුම 85, නිකුත් කිරීම 11, නොවැම්බර් 1997 පිටුව (s): - 1863 1857.
• " අතීතය පරිලෝකනය: අතීතයේ සිට විදුලි ඉංජිනේරු විද්යාව පිළිබඳ ඉතිහාසය ". IEEE Vol. 81, අංක 6, 1993.
• ෂෝසෝ උමාමි සහ ජෙන්ටී සැටෝ, " කෙටුම්පත කෙටි තරංග ඇන්ටනා, 1924 ". IEEE Milestones, IEEE ඉතිහාස මධ්යස්ථානය, IEEE, 2005.
• Pozar, David M. Microwave and RF Design of Wireless Systems. John Wiley & Sons Inc.

බාහිර සබඳතා

• Yagi-Uda ඇන්ටෙනා ඉතිහාසය ". ඇන්ටෙනා නව සොයාගැනීමේ ඉතිහාසය සහ එහි පේටන්ට් බලපත්ර.
• ඩී. ජෙෆරිස්, " යගි-යූඩා ඇන්ටනා සංරක්ෂණය කළ පිටපත 2005-12-25 at the Wayback Machine ". 2004.
• යගි-උඩ ඇන්ටනා . Yagi - Uda ඇන්ටෙනාහි මූලික සැලසුම, ව්යාපෘති සහ මිනුම් පිළිබඳ සරල තොරතුරු. 2008
• Yagi-Uda ඇන්ටනා www.antenna-theory.com