Fisica classica/Cinematica

Modulo precedente Indice

Torna a Fisica classica

Modulo successivo Dinamica

La meccanica riguarda lo studio del moto dei corpi, all'aumentare del loro numero lo studio diventa molto complicato, per questa ragione in meccanica, come in molti rami della fisica, in genere si studiano prima i sistemi semplici e poi quelli via via più complessi. Quindi nel nostro studio considereremo inizialmente il moto di un solo semplice corpo. Il più semplice corpo materiale è in realtà il punto materiale e da tale semplice corpo incominceremo lo studio della meccanica classica. La meccanica classica odierna nasce con le osservazioni sperimentali di Galileo Galilei che incomincia a studiare sperimentalmente il moto dei corpi. Nasce così la prima branca della meccanica: la cinematica.

La cinematica è quel ramo della Meccanica Classica che studia il moto dei corpi materiali dal punto di vista puramente geometrico, senza occuparsi di studiare le cause che hanno prodotto quel tipo particolare di moto. Di quest'ultimo aspetto si occupa la Dinamica che, in meccanica classica d'impostazione newtoniana, tratta le forze e i loro effetti sul moto.

Tempo

Uno dei punti di partenza della Meccanica Classica è il postulato sull'esistenza del tempo come grandezza continua e uniforme. Queste caratteristiche sono individuabili intuitivamente dal senso comune e possono essere così delineate con una discussione di tipo fenomenologico-metafisico:

1. Continuità del tempo: il tempo fluisce in modo continuo e non a scatti (come la lancetta dei secondi ad esempio) ovvero osserviamo lo scorrere continuo del tempo come un fluido continuo (Eraclito) e non fotogramma per fotogramma.
2. Uniformità del tempo: il tempo fluisce in modo uniforme e sempre nello stesso verso, non si osservano infatti rapporti inversi di causa-effetto o fenomeni come il déjà-vu cari alla letteratura fantascientifica.

Per riassumere rigorosamente queste caratteristiche i fisici e i matematici hanno coniato un postulato fondamentale di esistenza del tempo che si può enunciare come segue:

"Esiste il tempo una variabile continua sempre crescente"

Ma riprendendo Feynman, non ci interessa definirlo ma come misurarlo. Un modo naturale di misurarlo è di utilizzare un fenomeno che si ripete regolarmente che quindi definiamo periodico. Il giorno è stata probabilmente la prima misura periodica usata per caratterizzare il tempo. Attualmente gli astronomi usano calcolare il tempo con il giorno giuliano che è il numero di giorni passati dal mezzogiorno del lunedì 1º gennaio 4713 a.C. allo scopo di unificare differenti cronologie storiche. Per altri scopi il giorno non è una buona unità di misura in quanto la durata cambia nel corso dell'anno e inoltre è poco adatta a descrivere fenomeni veloci.

Un orologio atomico su chip

L'unità di misura del sistema internazionale è il secondo (indicato con s), unità che è in qualche maniera riconducibile a un fenomeno periodico: il battito del cuore. Gli strumenti che misurano il tempo, che si basano sempre su fenomeni periodici, vengono chiamati orologi e lo sviluppo della precisione nella misura del tempo è stato un fenomeno costante nello sviluppo della società. Attualmente gli strumenti che misurano con assoluta precisione il tempo sono gli orologi atomici, tali strumenti hanno una accuratezza di una parte su $10^{16}\$: cioè l'errore nella misura del tempo accumulato in un giorno è di appena $10^{-11}\ s\$. Il tempo è una delle grandezze fisiche misurabili con maggiore precisione.

Tempi brevi

In maniera artificiale sappiamo produrre segnali che hanno una durata molto breve; attualmente i laser sono gli oggetti artificiali che riescono a emettere impulsi cosi brevi come $1\ fs=10^{-15}\ s\$. Mentre riusciamo a misurare eventi che hanno una durata temporale molto più breve, vi sono infatti delle particelle instabili che hanno una vita media inferiore a $10^{-24}\ s$. La fisica moderna pone un limite inferiore alla descrizione degli intervalli temporali nel tempo di Planck $10^{-44}\ s$, per intervalli di tempo inferiore a tale tempo si dubita che il tempo conservi il suo carattere continuo. Ma tale tempo è molto lontano dai limiti sperimentali attuali.

Tempi lunghi

Il tempo più lungo immaginabile è di 13,8 miliardi di anni ($4\cdot 10^{17}\ s$): l'età dell'Universo. Il nostro sistema solare esiste da 4,5 miliardi di anni($1.4\cdot 10^{17}\ s$). Il primo uomo è comparso sulla Terra un milione di anni fa ($3\cdot 10^{13}\ s$) e così via fino a eventi di durata nota.

Spazio

Allo stesso modo si individua una grandezza chiamato spazio che ha le proprietà di continuità (come il tempo) e isotropia.

Per spiegare intuitivamente queste caratteristiche si può immaginare la continuità dello spazio come assenza di zone di inaccessibilità (a meno che non siano già occupate da un altro corpo). Possiamo spostare con continuità un oggetto mobile senza trovare dinanzi ostacoli inspiegabili e invisibili al suo moto. Ciò risulta possibile solo se lo spazio è dotato di continuità e non ha, per così dire, buchi. Ad esempio la materia di cui è composto un formaggio svizzero non è continua. Non possiamo spostarci in un formaggio svizzero mantenendoci sempre nel formaggio e senza cader in un buco. Se lo spazio reale avesse dei buchi, ovvero mancasse di continuità, potrebbero verificarsi brusche cadute (senza alcuna causa) oppure inspiegabili barriere trasparenti. Bisogna anche dire che in realtà, lontano dalla Terra e in prossimità dei buchi neri, lo spazio, come lo percepiamo sperimentalmente, perde la sua continuità. In prossimità di un buco nero infatti le traiettorie della luce che utilizziamo per fare le nostre misurazioni vengono deviate e la misura perde di significato nell'accezione della geometria euclidea. In questo caso possiamo supporre una perdita della continuità e dell'uniformità dello spazio che circonda il buco nero che pertanto viene indicato anche come una singolarità dello spazio.

L'isotropia è l'assenza di direzioni preferenziali nello spazio, ovvero lo spazio ci appare con le stesse proprietà geometriche in tutte le direzioni. Se un oggetto è rettilineo questo oggetto non appare curvo o di lunghezza diversa se viene spostato in un punto differente dello spazio. Anche questa accezione dello spazio (isotropia) è valida in Meccanica Classica ma non in generale in altre teorie fisiche più generali. In Cinematica ci si occupa solo di spazi che non creano troppi problemi, anzi più esattamente di spazi euclidei tridimensionali e quindi si assume come postulato lo spazio continuo, isotropo, euclideo, tridimensionale. Sussiste quindi, come per il tempo, il postulato seguente

"Esiste lo spazio grandezza continua, isotropa ed euclidea"

La distanza tra due punti dello spazio è una grandezza fisica chiamata lunghezza, l'unità di misura è il metro. In origine, durante la rivoluzione francese nel 1791, venne definito come 1/10 000 000 del meridiano terrestre fra il polo nord e l'equatore, cercando di rendere universale la grandezza. In realtà la misura non era precisa, e si preferì alla fine dell'ottocento utilizzare come campione la distanza tra due linee incise su una barra campione di platino-iridio conservata a Sèvres presso Parigi. Infine nel 1963, poiché la velocità della luce nel vuoto è una grandezza fondamentale della natura e poiché il tempo è misurabile con grandissima precisione, il metro viene definito come la distanza percorsa dalla luce nel vuoto in un intervallo di tempo pari a ${\frac {1}{299792458}}\ s$, assumendo che la velocità della luce nel vuoto, per definizione, è pari a $2,99792458\cdot 10^{8}\ m/s$.

Grandezze fisiche

Si intende come grandezza fisica una proprietà del mondo reale che può essere distinta qualitativamente e determinata quantitativamente. La scelta del numero di grandezze fisiche da cui fare derivare tutte le altre è abbastanza arbitrario. Circa 50 anni fa la maggior parte degli stati ha stabilito il cosiddetto sistema internazionale di unità di misura abbreviato in SI nel quale si sono scelte sette grandezze fisiche come fondamentali (lunghezza, tempo, massa, corrente, temperatura, intensità luminosa, mole). A ciascuna di queste grandezze è associato un simbolo dimensionale: lunghezza (L), tempo (T), massa (M), corrente (I), Temperatura (Θ), intensità luminosa (J), quantità di materia (N), e una unità di misura, per la lunghezza il metro (abbreviato in m) e per il tempo il secondo (abbreviato in s). Ogni altra grandezza fisica è derivata dal prodotto/rapporto di potenze di grandezze fondamentali. Il prodotto delle grandezze fisiche fondamentali è detto dimensione: ad esempio una superficie ha le dimensioni di una [L²], mentre un volume di una [L³], una velocità di [LT^-1]. L'analisi dimensionale è abitualmente usata per verificare la plausibilità di calcoli ed equazioni. Le altre grandezze fisiche fondamentali e quelle derivate verranno introdotte via via che serviranno. Gli argomenti di funzioni esponenziali, trigonometriche e logaritmiche devono essere adimensionali, cioè dei numeri puri.

Punto Materiale

La modellazione matematica del moto passa per una idealizzazione dei corpi materiali come percepiti dall'esperienza comune. In cinematica infatti, i corpi materiali, estesi nello spazio tridimensionale per loro natura, sono idealizzati geometricamente come contratti in un solo punto geometrico (ente geometrico zero-dimensionale). Questa idealizzazione è alla base del concetto di punto materiale che costituisce quindi una forte semplificazione della realtà tridimensionale ed estesa dei corpi materiali. La dinamica del corpo rigido descrive la complessità degli oggetti estesi come sistemi di punti materiali vincolati rigidamente tra di loro, consentendo una trattazione fisica completa di tali corpi estesi.

Traiettoria di un Punto Materiale

Le posizioni successive occupate dal punto materiale nello spazio al variare del tempo costituisce un insieme continuo di punti che prende il nome di traiettoria del punto materiale nello spazio.

Moto rettilineo

Cominciamo analizzando un semplice moto lungo la più semplice traiettoria: la retta, tale moto viene detto moto rettilineo. In questo caso possiamo studiare il moto attraverso delle grandezze caratteristiche scalari la posizione, la velocità e l'accelerazione.

Velocità

La rapidità con cui avviene lo spostamento lungo la traiettoria nel tempo determina una grandezza detta velocità media data dalla seguente relazione $v_{m}={\frac {x-x_{0}}{t-t_{0}}}={\frac {\Delta x}{\Delta t}}$. Dove $x_{0}\$ è la posizione al tempo $t_{0}\$ e $x\$ è la posizione al tempo $t\$.

Le dimensioni della velocità sono [v]=[LT^-1]. La velocità nel sistema SI si misura in m/s, mentre nel linguaggio comune viene utilizzato km/h. Nel fare i calcoli bisogna fare attenzione a dividere le velocità espresse in km/h per 3,6 per ottenere la velocità in m/s. Esiste una massima velocità possibile: la velocità della luce (c) che vale per definizione $2,99792458\cdot 10^{8}\ m/s$

Un semplice esempio può essere quello del moto di un'automobile che percorre 60 km in 30 minuti: essa avrà una velocità media di 120 km/h (quindi circa 33 m/s).

Possiamo chiederci quale potrebbe essere la velocità in ogni istante e per fare questo dovremo considerare piccolissimi intervalli di tempo, in pratica dovremo far tendere $\Delta t\,\!$ a zero. La velocità così ottenuta è detta velocità istantanea e rappresenta la rapidità di variazione della posizione all'istante scelto.

Questa è data quindi dalla derivata dello spazio percorso rispetto al tempo:

$v(t)={\frac {dx}{dt}}$

e se volessimo trovare lo spazio percorso dall'istante iniziale all'istante $t$ non dovremmo far altro che utilizzare le regole di integrazione e quindi:

$dx=v(t)dt\Rightarrow \int _{x_{0}}^{x}dx'=\int _{t_{0}}^{t}v(t')dt'\Rightarrow x-x_{0}=\int _{t_{0}}^{t}v(t')dt'\Rightarrow x(t)=x_{0}+\int _{t_{0}}^{t}v(t')dt'$

Questa è la regola generale che mette in relazione la velocità con lo spazio percorso. Notiamo come dalla conoscenza della legge oraria cioè x(t), lo spazio percorso in funzione del tempo, la determinazione della velocità istantanea è definita in maniera univoca. Mentre se conosciamo l'andamento della velocità in funzione del tempo la posizione la possiamo determinare in maniera relativa, in quanto qualsiasi posizione iniziale determina lo stesso andamento della velocità, quindi va specificata a un certo tempo quale sia la posizione per rimuovere tale relativismo.

Moto rettilineo uniforme

Questo è il caso più semplice in cui la velocità istantanea e la velocità media coincidono e valgono $v\$, l'equazione del moto cioè la relazione tra la posizione istantanea $x(t)\$ e il tempo è:

$x(t)=x_{0}+v(t-t_{0})\$

(1)

Questo moto si chiama moto rettilineo uniforme. $x_{0}\$ è la posizione all'istante iniziale, cioè quando $t=t_{0}\$.

Accelerazione

Lo stesso ragionamento può essere fatto con la velocità: infatti anch'essa potrebbe variare nel tempo e il tasso di variazione è dato da una grandezza chiamata accelerazione. La accelerazione ha le dimensioni di [LT^-2] e nel sistema SI si misura in ms^-2. Anche per l'accelerazione possiamo definire una accelerazione media e una accelerazione istantanea date dalle seguenti relazioni $a_{m}={\frac {\Delta v}{\Delta t}}$ e

$a(t)={\frac {dv}{dt}}$

Anche per l'accelerazione, integrando otteniamo la relazione che la lega alla velocità:

$dv=a(t)dt\Rightarrow \int _{v_{0}}^{v}dv'=\int _{t_{0}}^{t}a(t')dt'\Rightarrow v-v_{0}=\int _{t_{0}}^{t}a(t')dt'\Rightarrow v(t)=v_{0}+\int _{t_{0}}^{t}a(t')dt'$

e anche in questo caso se $v_{0}=0\,\!$, $a=costante\,\!$ e si partisse al tempo $t_{0}=0\,\!$ avremmo la relazione $v=at\,\!$ che definisce un moto uniformemente accelerato

Moto uniformemente accelerato

Combinando i risultati ottenuti e considerando $v\,\!$ e $a\,\!$ costanti possiamo ottenere la legge che definisce il moto uniformemente accelerato

$x(t)=x_{0}+v_{0}(t-t_{0})+{\frac {1}{2}}a(t-t_{0})^{2}$

(2)

Qui $v_{0}\$ è la velocità all'istante iniziale. Se $t_{0}=0\,\!$, l'equazione diviene

$x(t)=x_{0}+v_{0}t+{\frac {1}{2}}at^{2}\$

(3)

La relazione tra la posizione spaziale e il tempo di cui abbiamo visto due semplici esempi è chiamata equazione oraria.

Alcuni esempi possono essere di aiuto per comprendere quanto detto: Moto di un elettrone, Automobile, Treno, Rally.

Caduta verticale dei gravi

Se viene trascurato l'attrito dell'aria ogni corpo lasciato libero di cadere in vicinanza della superficie terrestre si muove lungo una traiettoria rettilinea con accelerazione costante $g=9,8\ m/s^{2}$. La legge oraria che descrive la caduta dei gravi è quella tipica del moto uniformemente accelerato con $t_{0}=0\,\!$:

$x(t)=x_{o}+v_{o}t-{\frac {1}{2}}gt^{2}$

(4)

Assunto come positiva la verticale uscente dal suolo, quindi il segno negativo nella accelerazione è dovuto al fatto che il corpo si sta muovendo contrariamente al verso scelto come positivo nel sistema di riferimento.

Un esempio di questo caso è una palla lanciata verso l'alto, o la stima della profondità di un pozzo facendo cadere un sasso.

Moto armonico semplice

Moto armonico

Questo tipo di moto è molto comune in molti sistemi fisici e in genere prende il nome di oscillatore armonico. Da un punto di vista algebrico la sua legge oraria è descritta da:

$x(t)=A\cos(\omega t+\theta _{0})\,\!$

(5)

Dove $A\,\!$ è detta ampiezza del moto, $\omega \,\!$ pulsazione e $\theta _{0}\,\!$ la fase iniziale.

A causa delle proprietà della funzione seno la posizione oscilla tra -A e A. All'istante iniziale la posizione è:

$x_{o}=A\cos(\theta _{0})\,\!$

Il moto è chiaramente periodico con periodo $T\,\!$ cioè:

$\omega (t+T)+\theta _{0}=\omega (t)+\theta _{0}+2\pi \,\!$

da cui:

$T={\frac {2\pi }{\omega }}\,\!$

(6)

L'inverso del periodo si chiama frequenza ha le dimensioni di un $[T^{-1}]\,\!$ e si misura in hertz (abbreviato in Hz):

$\nu ={\frac {1}{T}}$

Derivando la legge del moto si ha l'equazione della velocità del punto:

$v(t)={\frac {dx}{dt}}=A\omega \cos(\omega t+\theta _{0})\,\!$

La velocità ora è massima al centro di oscillazione, ed è nulla dove l'allontanamento dalla posizione centrale è massima.

Derivando ulteriormente si ottiene l'accelerazione del punto:

$a(t)={\frac {dv}{dt}}={\frac {d^{2}x}{dt^{2}}}=-A\omega ^{2}\sin(\omega t+\theta _{0})\,\!$

Confrontando l'ultima equazione e la prima segue che:

${\frac {d^{2}x}{dt^{2}}}=-\omega ^{2}x\,\!$

(7)

Cioè necessariamente nel moto armonico l'accelerazione è proporzionale alla posizione istantanea cambiata di segno e la costante di proporzionalità è il quadrato della pulsazione. L'ampiezza di oscillazione come la fase iniziale sono determinate dalle condizioni iniziali del moto.

Due esempi possono servire a mettere in chiaro quanto detto: il primo caso è un semplice moto armonico, il secondo è il calcolo della ampiezza di oscillazione a partire da alcuni dati cinematici.

Moto nello spazio

La posizione di un oggetto nello spazio, come la sua velocità e accelerazione sono delle grandezze vettoriali, rappresentate come segmenti orientati. Nel caso della posizione si rappresenta con un segmento orientato con un estremo sull'origine e l'altro estremo sulla posizione istantanea del punto materiale nello spazio.

L'algebra dei vettori viene utilizzata per caratterizzare la dinamica nello spazio, e qui non vengono definiti gli elementi di tale algebra e saranno utilizzate come note la definizione di somma di vettori (regola del parallelogramma), la moltiplicazione per uno scalare, il prodotto scalare e quello vettoriale.

Un vettore può essere espresso come somma di componenti lungo tre direzioni ortogonali (gli assi cartesiani).

Versore

La variazione nel tempo di un versore in coordinate polari.

Nel concetto di spazio vettoriale è essenziale il concetto di versore cioè un vettore unitario, un versore si indica con ${\hat {u}}$. Essendo unitario: ${\hat {u}}\cdot {\hat {u}}=1$.

Ma notiamo come derivando l'espressione precedente si ha che:

$0={\frac {d({\hat {u}}\cdot {\hat {u}})}{dt}}=2{\hat {u}}\cdot {\frac {d({\hat {u}})}{dt}}$

Quindi la derivata di un versore è un vettore normale al versore originale o un vettore nullo. Solo se il versore non cambia di direzione nel tempo il valore della sua derivata è nullo, ma se il versore cambia di direzione la derivata può assumere un valore diverso da zero. La derivta di un versore non è in genere un versore. Che la derivata di un versore sia normale alla direzione del versore stesso, è anche evidente dalla figura a fianco in cui si precisa meglio il valore della derivata che è dato da:

${\frac {d{\hat {u}}}{dt}}={\frac {d\varphi }{dt}}{\hat {u}}_{\varphi }$

(8)

dove $\varphi \,\!$ è l'angolo infinitesimo e $u_{\varphi }$ è la componente normale alla direzione del versore.

Vettore di posizione

Quantità cinematiche di un punto materiale: massa m, posizione r, velocità v, accelerazione a.

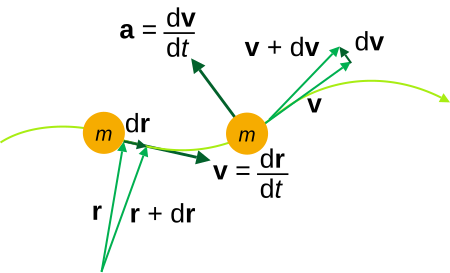
Se $O$ è la posizione dell'osservatore e $P$ la generica posizione di un punto materiale nello spazio geometrico, si definisce vettore di posizione il vettore ${\vec {r}}$ rappresentato dal segmento orientato ${\vec {OP}}$. Per indicare questa corrispondenza in questa trattazione si utilizzerà la scrittura ${\vec {r}}\sim {\vec {OP}}$. Il vettore di posizione dipende dalla scelta del punto di osservazione $O$, quindi è un segmento orientato, ma la sua definizione permette di costruire delle quantità che sono indipendenti dalla scelta del punto di osservazione. Queste quantità sono la velocità e l'accelerazione vettoriale.

Posizione

Per definire la posizione di un corpo è necessario definire un sistema di riferimento, come ad esempio un sistema di due assi cartesiani la cui origine è scelta in maniera arbitraria. Si può definire lo spostamento in funzione del tempo facendo corrispondere a ogni t una posizione (x,y) nel piano:

${\vec {r}}(t)=x(t){\hat {\imath }}+y(t){\hat {\jmath }}$

Avendo indicato con ${\hat {\imath }}$ e ${\hat {\jmath }}$, i versori degli assi x e y.

Sistemi di coordinate

Confronto tra coordinate cartesiane e polari nel piano.

Il sistema di coordinate usato finora implicitamente è un sistema di assi cartesiani in due dimensioni. In alcuni casi dotati di particolari proprietà di simmetria è preferibile usare nel piano un sistema che identifica la distanza r del punto dall'origine degli assi chiamata raggio vettore e dall'angolo $\theta \,\!$ formato con l'asse delle ascisse. Un sistema di questo genere si chiama sistema polare nel piano. La figura a fianco mette in evidenza la relazione tra coordinate cartesiane e polari nel piano. Di conseguenza le relazioni tra i due sistemi di coordinate sono le seguenti:

$x=r\cdot \cos \theta \$

$y=r\cdot \sin \theta \$

$r={\sqrt {x^{2}+y^{2}}}\$

$\theta =\arctan {\frac {y}{x}}\$

Moto nel piano

Analizziamo ora la posizione di un punto che in un tempo t percorre un tratto di traiettoria.

Le posizioni sono ${\vec {r}}(t)$ e ${\vec {r}}(t+\Delta t)$; la distanza tra di essi è ${\vec {\Delta r}}={\vec {r}}(t+\Delta t)-{\vec {r}}(t)$, di conseguenza la velocità media (diventata una grandezza vettoriale) è data da:

${\vec {v}}_{m}={\frac {{\vec {r}}(t+\Delta t)-{\vec {r}}(t)}{\Delta t}}$

Notiamo che la distanza dei punti non coincide con la traiettoria percorsa, ma è solo la misura della distanza tra le due posizioni su un piano. Ma se noi facessimo tendere $\Delta t\to 0$ avremmo che

${\vec {v}}={\frac {d{\vec {r}}}{dt}}$

e il vettore $d{\vec {r}}$ diventa tangente alla traiettoria e coincide in modulo con l'infinitesimo spostamento $ds\,\!$.

Se ne ricava allora che $d{\vec {r}}=ds\cdot {\hat {u}}_{T}$ dove ${\hat {u}}_{T}$ non è altro che il versore (un vettore unitario) che dà la direzione dello spostamento.

Ricaviamo così che ${\vec {v}}={\frac {ds}{dt}}\cdot {\hat {u}}_{T}=v\cdot {\hat {u}}_{T}$ e quindi possiamo dedurre che la velocità vettoriale individua in ogni istante la direzione e il verso del movimento e ci dà la velocità istantanea $v={\frac {ds}{dt}}$ con la quale è percorsa la traiettoria.

Velocità in coordinate cartesiane

Nelle coordinate cartesiane il vettore posizione:

${\vec {r}}=x{\vec {i}}+y{\vec {j}}\$

Quindi:

${\vec {v}}={\frac {d{\vec {r}}}{dt}}={\frac {dx}{dt}}{\vec {i}}+{\frac {dy}{dt}}{\vec {j}}=v_{x}{\vec {i}}+v_{y}{\vec {j}}$

Quindi il modulo della velocità:

$v={\sqrt {v_{x}^{2}+v_{y}^{2}}}$

Mentre l'angolo che la velocità ha con l'asse delle x vale:

$\theta =\arctan {v_{y}/v_{x}}$

Velocità in coordinate polari

Nelle coordinate polari il vettore posizione:

${\vec {r}}=r{\hat {u}}_{r}\$

Dove ${\hat {u}}_{r}$ è il versore radiale (normale al versore ${\hat {u}}_{T}$ tangenziale). Quando andiamo a fare la derivata:

${\vec {v}}={\frac {d{\vec {r}}}{dt}}={\frac {dr}{dt}}{\hat {u}}_{r}+r{\frac {d{\hat {u}}_{r}}{dt}}\$

La derivata del versore è nella direzione normale alla direzione radiale. Se la traiettoria cambia di direzione vi è oltre alla velocità trovata nel moto lineare, una componente non nulla della velocità nella direzione ortogonale al vettore posizione in definitiva:

${\vec {v}}={\frac {dr}{dt}}{\hat {u}}_{r}+r{\frac {d\theta }{dt}}{\hat {u}}_{\theta }=v_{r}{\hat {u}}_{r}+v_{\theta }{\hat {u}}_{\theta }\$

La velocità è tangente alla traiettoria e si compone di una parte radiale (${\frac {dr}{dt}}\$) e una trasversa ($r{\frac {d\theta }{dt}}\$) e quindi il modulo della velocità vale:

$v={\sqrt {\left({\frac {dr}{dt}}\right)^{2}+r^{2}\left({\frac {d\theta }{dt}}\right)^{2}}}\$

(9)

Analogamente a quanto detto per il moto rettilineo integrando l'espressione ${\vec {v}}={\frac {d{\vec {r}}}{dt}}$ otteniamo quella generale che collega posizione e velocità data da

${\vec {r}}(t)={\vec {r}}(t_{0})+\int _{t_{0}}^{t}{\vec {v}}(t)dt$

Accelerazione

Esempio di costruzione del cerchio osculatore

La derivata della velocità rispetto al tempo è la accelerazione nel moto piano:

${\vec {a}}={\frac {d{\vec {v}}}{dt}}={\frac {d}{dt}}(v{\vec {u}}_{T})={\frac {dv}{dt}}{\vec {u}}_{T}+v{\frac {d{\vec {u}}_{T}}{dt}}={\frac {dv}{dt}}{\vec {u}}_{T}+v{\frac {d\theta }{dt}}{\vec {u}}_{N}$

(10)

Il primo termine parallelo alla traiettoria è analogo a quello trovato nel moto rettilineo ed è una misura di quanto vari nel tempo il modulo della velocità. Il secondo termine è legato al cambiamento di direzione e quindi è tanto maggiore quanto più grande è l'allontanamento dal moto rettilineo. Il modo più idoneo per esprimere tale allontanamento è di approssimare localmente la traiettoria con una circonferenza e studiare il moto localmente come un moto circolare. Da un punto di vista analitico si approssima localmente la traiettoria con una circonferenza, detta cerchio osculatore. Ciò matematicamente è possibile in quanto per tre punti passa una unica circonferenza, cioè con raggio e centro definiti in maniera univoca, anche nel caso limite dei tre punti allineati ciò è possibile in quanto il cerchio osculatore ha un raggio infinito e centro all'infinito. La figura a fianco mostra un tipico cerchio osculatore. Quindi è opportuno prima considerare un particolare moto nel piano: quello circolare. Infatti le proprietà del moto circolare descrivono il moto più generale nel piano con cerchi osculatori che variano nel tempo.

Un primo esempio di tale moto è il moto ellittico studiato in forma parametrica, un seconda traiettoria è una spirale piana.

Moto circolare

Moto circolare.

Analizziamo un moto che si svolge su una traiettoria costituita da una circonferenza di raggio $R\$.

Introduciamo il concetto di velocità angolare $\omega \$: si chiama velocità angolare la derivata nel tempo dell'angolo (quindi la rapidità di variazione dell'angolo):

$\omega ={\frac {d\theta }{dt}}\$

Notiamo che si usa un simbolo simile alla pulsazione, ma ha un significato fisico diverso, anche se ha le stesse dimensioni di fisiche cioè un $t^{-1}\$. Il legame tra velocità angolare e velocità nel caso del moto circolare è chiaro, infatti a uno spostamento $ds=vdt\$ corrisponde un variazione angolare $d\theta =\omega dt\$, ma in una circonferenza $ds=Rd\theta =R\omega dt=vdt\$, quindi:

$v=\omega R\qquad \omega ={\frac {v}{R}}\$

Esaminiamo prima un caso più semplice il moto circolare uniforme, cioè un moto in cui $v\$ e di conseguenza $\omega \$ non variano nel tempo e il periodo, cioè il tempo necessario a compiere un giro vale:

$T={\frac {2\pi R}{v}}={\frac {2\pi }{\omega }}\$

La frequenza vale $\nu =1/T\$.

velocità v e accelerazione a nel moto circolare uniforme con velocità angolare ω; la velocità è costante, ma la velocità è sempre tangente all'orbita: la accelerazione è costante in valore assoluto, ma punta sempre verso il centro di rotazione.

Per quanto riguarda l'accelerazione la costanza della velocità fa sì che il termine dell'accelerazione tangenziale ${\frac {dv}{dt}}\$ sia nullo, cioè non varia in modulo la velocità, ma varia la sua direzione. In questo caso l'unica componente della accelerazione è la componente normale alla traiettoria diretta verso il centro della circonferenza:

$|a|={\frac {v^{2}}{R}}=\omega ^{2}R\$

(11)

In questo caso il sistema di coordinate più naturale è quello polare in cui il centro della circonferenza è il centro delle coordinate. In tale sistema si ha che:

$\theta (t)=\omega t+\theta _{o}\$

Dove $\theta _{0}\$ è l'angolo nell'istante iniziale ($t=0\ s$) con l'asse delle ascisse.

Notiamo che la proiezione del moto circolare uniforme sui due assi cartesiani:

$x(t)=R\cos(\theta )=R\cos(\omega t+\theta _{o})\$

$y(t)=R\sin(\theta )=R\sin(\omega t+\theta _{o})\$

siano due moti armonici di pari ampiezza e sfasati di un quarto di periodo.

Se il moto è circolare, ma non uniforme, avremo che bisogna introdurre anche la accelerazione angolare cioè:

$\alpha ={\frac {d\omega }{dt}}={\frac {1}{R}}{\frac {dv}{dt}}\$

Quindi l'espressione generale dell'accelerazione nel moto piano

${\vec {a}}={\frac {dv}{dt}}{\vec {u}}_{T}+v{\frac {d\theta }{dt}}{\vec {u}}_{N}=\alpha R{\vec {u}}_{T}+\omega ^{2}R{\vec {u}}_{N}$

(12)

Dove il secondo termine è la accelerazione centripeta che abbiamo già visto nel moto circolare uniforme, mentre il primo termine lungo la traiettoria è l'accelerazione tangenziale.

Un caso semplice che ricorda il moto uniformemente accelerato è il caso in cui $\alpha \$ è costante in tal caso avremo che l'equazione del moto per l'angolo è:

$\theta =\theta _{o}+\omega _{o}t+{\frac {1}{2}}\alpha t^{2}$

(13)

Dove $\theta _{o}\$ è l'angolo al tempo 0 e $\omega _{o}\$ è la velocità angolare al tempo 0. Quindi la velocità angolare:

$\omega =\omega _{o}+\ \alpha t$

In questo caso la accelerazione tangenziale è costante e vale $\alpha R\$, mentre quella centripeta vale $(\omega _{o}+\ \alpha t)^{2}R\$.

Velocità angolare - Notazione vettoriale

Velocità angolare.

La velocità angolare può essere descritta da una quantità vettoriale che definisce il verso di percorrenza sulla circonferenza e il modulo. La direzione di questo vettore è perpendicolare al piano del moto e il verso è dato dalla regola della mano destra, ovvero se il moto avviene nella direzione in cui si avvolgono le dita della mano destra la direzione $\omega \$ è il pollice della mano destra.

${\vec {v}}={\vec {\omega }}\times {\vec {r}}$

(14)

Se durante il moto la velocità angolare non cambia di direzione, la sua derivata rimane parallela alla direzione di ${\vec {\omega }}\$. Questa relazione ci permette di ottenere l'accelerazione del moto circolare dalla velocità angolare e dall'accelerazione angolare tramite la seguente relazione derivando semplicemente tale prodotto vettoriale:

${\vec {a}}={\frac {d{\vec {v}}}{dt}}={\frac {d}{dt}}({\vec {\omega }}\times {\vec {r}})={\frac {d{\vec {\omega }}}{dt}}\times {\vec {r}}+{\vec {\omega }}\times {\frac {d{\vec {r}}}{dt}}$

e quindi

${\vec {a}}=\alpha \times {\vec {r}}+{\vec {\omega }}\times {\vec {v}}={\vec {a}}_{T}+{\vec {a}}_{N}$

Quindi con questa notazione che non aggiunge niente dal punto di vista fisico, appare chiaro come il primo termine rappresenti la accelerazione tangenziale (cioè parallela alla traiettoria) e il secondo termine sia la accelerazione centripeta cioè diretta verso il cento di rotazione.

Moto parabolico

Moto parabolico da una altezza di $200\ m\$, con stessa velocità iniziale $50m/s\$ e con una accelerazione diretta verso il basso di $10m/s^{2}\$ al variare dell'angolo rispetto alla direzione orizzontale

Questa è l'estensione in due dimensioni del moto accelerato uniforme, ad esempio la caduta dei gravi; in questo caso la direzione della accelerazione non varia nel tempo oltre a essere costante in modulo. Il moto di questo tipo non riguarda solo la caduta dei gravi, ma tutte le situazioni dinamiche, come vedremo, in cui vi sia una forza costante in modulo e verso.

In questo caso la scelta più naturale degli assi è quella degli assi cartesiani e si assume come asse delle $y\$ la direzione della accelerazione $a\$. Se chiamiamo $\alpha \$ l'angolo che la velocità iniziale ha con la direzione orizzontale, le equazioni del moto sono in coordinate cartesiane:

$x(t)=(v_{o}\cos \alpha )t$

$y(t)=h+(v_{o}\sin \alpha )t-{\frac {1}{2}}gt^{2}\$

scelta la posizione iniziale sull'asse delle $y\$ con altezza iniziale $h\$ ($200\ m\$ nella figura); $v_{o}\$ è il modulo della velocità iniziale (nell'esempio della figura vale $50m/s\$). Quindi in una direzione è un moto rettilineo uniforme, nella direzione verticale è un moto accelerato uniforme.

La traiettoria viene ricavata eliminando il tempo dal sistema di due equazioni:

$y(x)=h+x\tan \alpha -{\frac {gx^{2}}{2v_{o}^{2}\cos ^{2}\alpha }}\$

(15)

la curva che descrive la traiettoria è quindi una parabola.

Si chiama gittata (x_G) la distanza tra la posizione iniziale e il punto in cui la traiettoria arriva a quota zero, cioè quando:

$h+x_{G}\tan \alpha -{\frac {gx_{G}^{2}}{2v_{o}^{2}\cos ^{2}\alpha }}=0\$

Escludendo dal sistema di secondo grado la soluzione negativa (in quanto si suppone che prima di $t=0\$ non vi sia moto), si ha che:

$x_{G}={\frac {v_{o}\cos \alpha }{g}}\left[v_{o}\sin \alpha +{\sqrt {v_{o}^{2}\sin ^{2}\alpha +2gh}}\right]\$

Con i dati in figura risulta (facendo il calcolo numerico) che la gittata massima è di $400\ m\$ (con un angolo di $33^{o}\$). Notare come, in questo caso, la soluzione analitica non sia banale, la soluzione si è trovata analizzando quando si annula la derivata della gittata rispetto all'angolo.

Un'altra informazione importante che si ricava dalla traiettoria è l'altezza massima che coincide ovviamente con $h\$ nel caso di angoli di lancio negativi. Se l'angolo è positivo e quindi la parabola ha il termine lineare positivo e quello quadratico negativo chiaramente la parabola ha un massimo che si ricava imponendo che la derivata di $y(x)\$ sia nulla:

${\frac {dy}{dx}}=0\qquad \longrightarrow x_{M}-x_{o}={\frac {v_{o}^{2}}{g}}\cos \alpha \sin \alpha \quad y_{M}=h+{\frac {1}{2}}{\frac {v_{o}^{2}\sin ^{2}\alpha }{g}}\$

Indicando con x_M ed y_M le coordinate del massimo, che dipendono ovviamente dall'angolo di lancio.

Moto nello spazio tridimensionale

Questo caso generale è più difficile da trattare, in quanto la traiettoria non ha una espressione analitica semplice: una linea nello spazio tridimensionale nasce dall'intersezione di due superfici, quindi si esprime come un sistema di due equazioni in tre variabili.

In coordinate cartesiane il vettore posizione in forma parametrica (con parametro il tempo) è:

${\vec {r}}(t)=x(t){\hat {\imath }}+y(t){\hat {\jmath }}+z(t){\hat {k}}$

La velocità (che continua a essere parallela alla traiettoria):

${\vec {v}}={\frac {d{\vec {r}}}{dt}}={\frac {dx}{dt}}{\hat {\imath }}+{\frac {dy}{dt}}{\hat {\jmath }}+{\frac {dz}{dt}}{\hat {k}}=v_{x}{\hat {\imath }}+v_{y}{\hat {\jmath }}+v_{z}{\hat {k}}$

E infine l'accelerazione (la cui direzione nel caso generale ha tutte le componenti possibili):

${\vec {a}}={\frac {d{\vec {v}}}{dt}}={\frac {d^{2}x}{dt^{2}}}{\hat {\imath }}+{\frac {d^{2}y}{dt^{2}}}{\hat {\jmath }}+{\frac {d^{2}z}{dt^{2}}}{\hat {k}}=a_{x}{\hat {\imath }}+a_{y}{\hat {\jmath }}+a_{z}{\hat {k}}$

In genere il moto tridimensionale si tratta in alcuni casi specifici, che sono sono combinazioni di moti nel piano e semplici nelle direzione perpendicolare, ad esempio la combinazione del moto circolare uniforme in un piano e del moto rettilineo uniforme dà luogo al cosiddetto moto elicoidale.

Note

Bibliografia

• Paolo Mazzoldi, Massimo Nigro, Cesare Voci, Fisica, vol. 1, 2ª ed., Edises, 2000, ISBN 8879591371.

Argomento seguente: Dinamica